线性插值

最近在看Canvas的一些动画实例当中，时常看到lerp()这个函数，一直以来并不知道这个函数起什么作用，有什么特性。今天花了一些时间，Google了一下，才知道这个函数是线性插值。那么线性插值是个什么鬼？他在一些程序中又起啥作用？这就是这篇文章要探讨和学习的。

什么是线性插值

线性插值是数学、计算机图形学等领域广泛使用的一种简单插值方法。在平常实际运用当中，把插值称之为lerp。简单而言：

lerp是两点之间的线性插值的别称。

在深入了解之前，有几个小概念先介绍一下：

• 内插：内插是数学领域数值分析中的通过已知的离散数据求未知数据的过程或方法
• 拟合：根据若干离散的数据，得到一个连续的函数（也就是曲线）或者更加密集的离散方程与已知数据相吻合

也就是说：内插是曲线必须通过已知点的拟合。

在离散数据的基础上补差连续函数，使用这条连线曲线通过全部的离散数据点。插值是离线函数逼近的重要方法，利用它可通过函数在有限个点处的取值状况，估算出函数在其他点处的近似值。

时常看到的插值主要分为：线性插值、双线线性插值和三线性插值。虽然插值有多种类型，但我们今天要聊的也只是其中的一种，那就是最简单的插值——线性插值。

如何进行线性插值

假设我们已知A点的坐标(x0,y0)与B点的坐标(x1,y1)，要得到[x0, x1]区间内某一位置x在直线上的值，比如下图中的(x,y)：

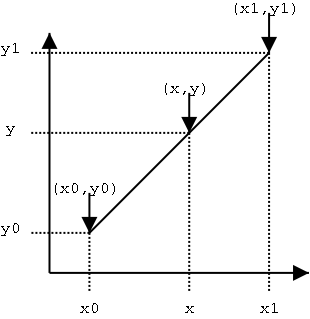
根据图中所示，我们可以得到：

(y - y0) / (x - x0) = (y1 - y0) / (x1 - x0)

由于x值已知，所以可以从公式中得到y的值：

y = y0 + (x - x0) * (y1 - y0) / (x1 - x0) = y0 + ((x - xo) * y1 - (x - x0) * y0) / (x1 - x0)

同样的，根据上面的公式，已知y的值，可以求出x的值。

插值的运用

线性插值经常用于补充表格中的间隔部分。两值之间的线性插值基本运算在计算机图形学中的应用非常普遍，以至于在计算机图形学领域的行话中人们将它称之为lerp。所有当今计算机图形处理器的硬件中都集成了线性插值运算，并且经常用来组成更为复杂的运算。例如，可以通过三步线性插值完成一次双线性插值运算。由于这种运算成本较低，所以对于没有足够数量条目的光滑函数来说，它是实现精确快速查找表的一种非常好的方法。

我们在常用的骨骼动画、物体移动、灯光渐隐、摄像机动画和图形渲染中都会用到插值。接下来，我们看代码中怎么使用线性插值（前面也说了，我们这里只说线性插值）.

线性插值

假如我们需要将物体x通过n步，从A点移动到B点，可以使用下面的代码：

for (var i = 0; i < n; i++) {
    x = ((A * i) + (B * (n - i))) / n;
}

或者：

for (var i = 0; i < n; i++) {
    v = i / n;
    x = (A * v) + (B * (1 - v));
}

可以看到v的取值范围是0~1，插值中我们均可归一化至0 ~ 1范围内。

用n个离散学将0移动至1称为线性插值lerp。

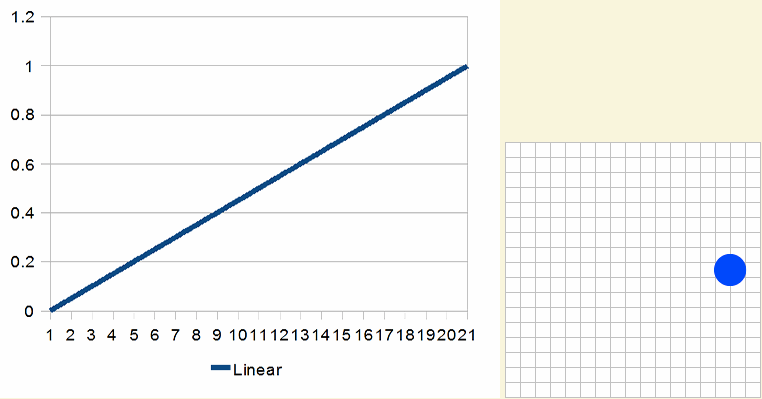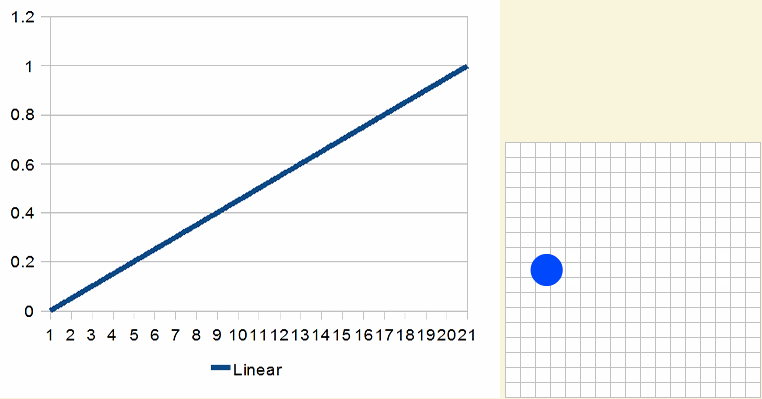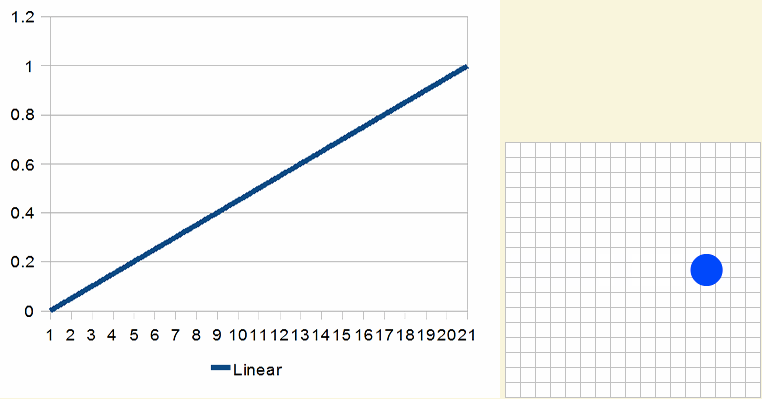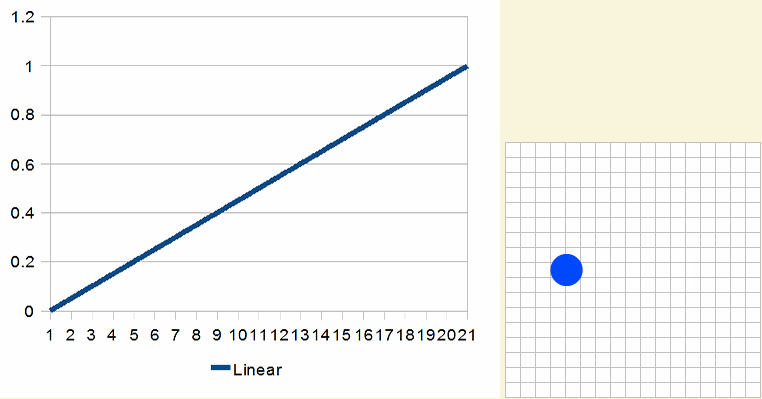
上面的移动动画效果是不是看上去生效，非常不和谐。如果将这样的动效运用到我们实际项目当中，特别是一些游戏人物行走，肯定无法达到需求方的要求。事实上，我们还是有方法可以进行修正的。

Smoothstep

前面那样使用，让动效看上去比较生硬，那么我们在上面的基础上考虑一下下面这个平滑函数：

function smoothstep(x) {
    return (x * x * (3 - 2 * x));
}

上面公式怎么来的，其实底层我也说不清楚，不过维基百科做出详细的介绍。如此一来，上面的lerp函数就可以改成：

for (var i = 0; i < n; i++) {
    v = i / n;
    v = smoothstep(v);
    x = (A * v) + (B * (1 - v));
}

这样效果会变得更平滑些。不过我们可以使用smootherstep

function smootherstep(x) {
    return x * x * x * (x * (x * 6 - 15) + 10);
}

Smoothstep效果看起来像下图：

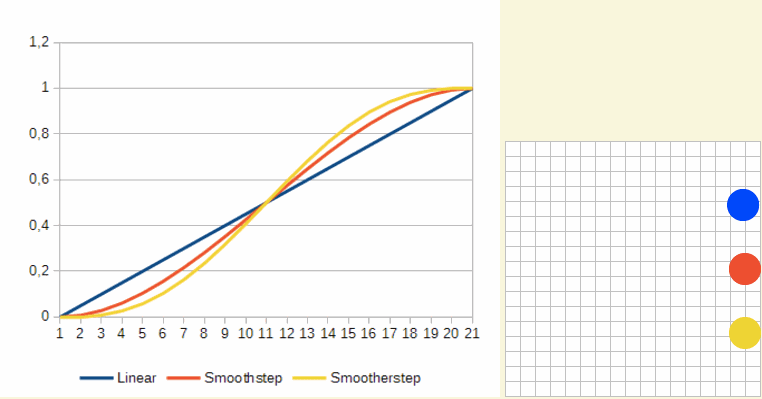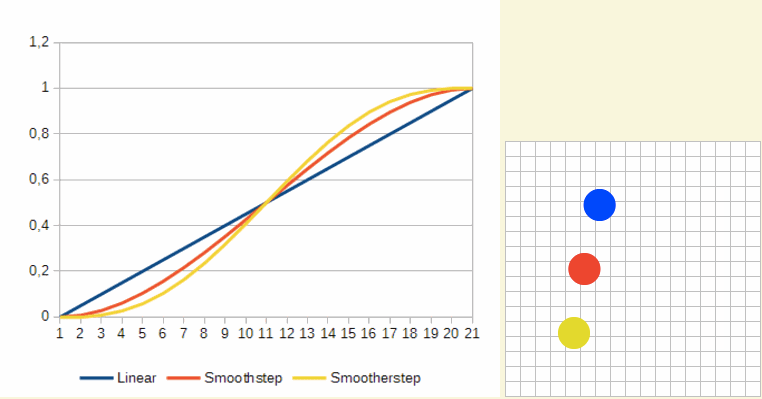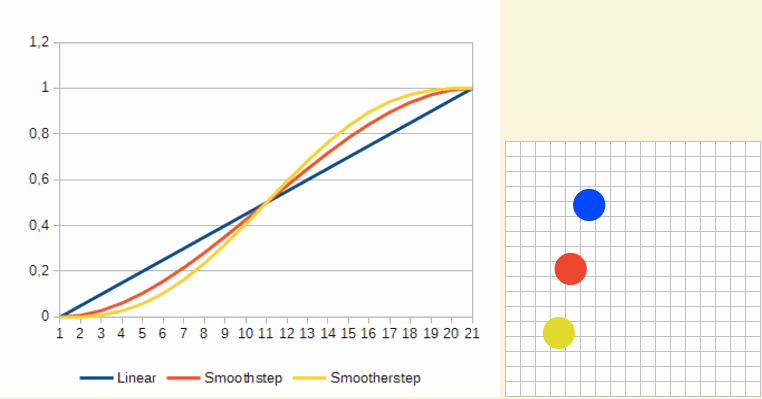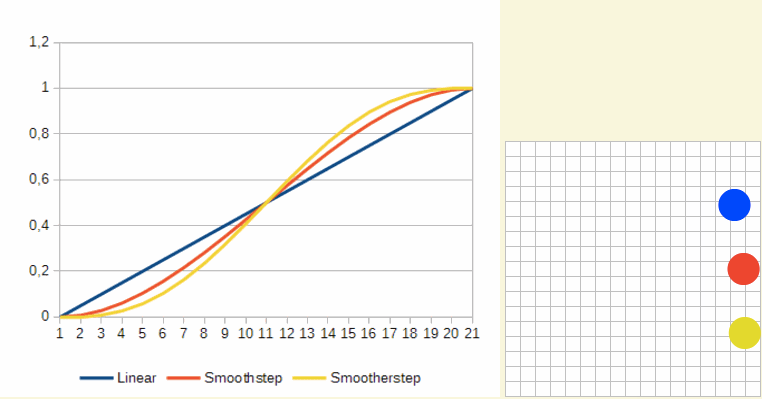
这样效果自然多了，是不是。当快接近目标时移动会慢下来。

高次幂

如果运动时想有缓慢加速效果，简单利用n次幂就可以：

for (var i = 0; i < n; i++) {
    v = i / n;
    v = v * v;
    x = (A * v) + (B * (1 - v));
}

如果运动时想有缓慢减速，上面的公式反相即可：

for (var i = 0; i < n; i++) {
    v = i / n;
    v = 1 - (1 - v) * (1 - v);
    X = (A * v) + (B * (1 - v));
}

这些效果看起来像下面这样：

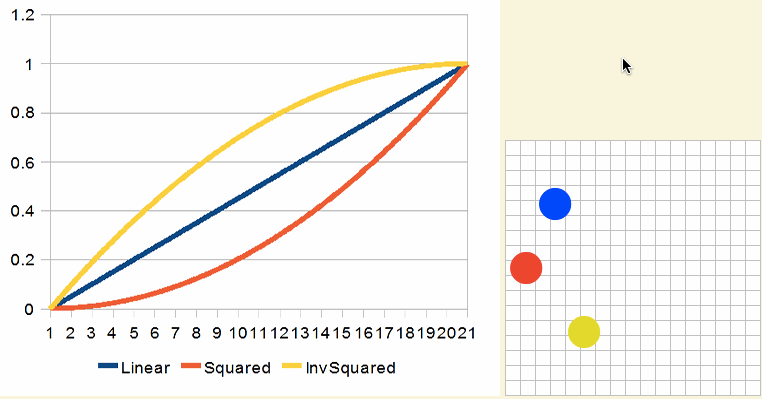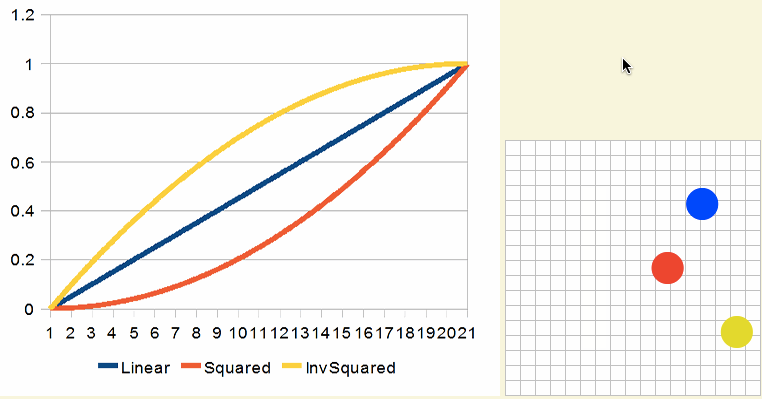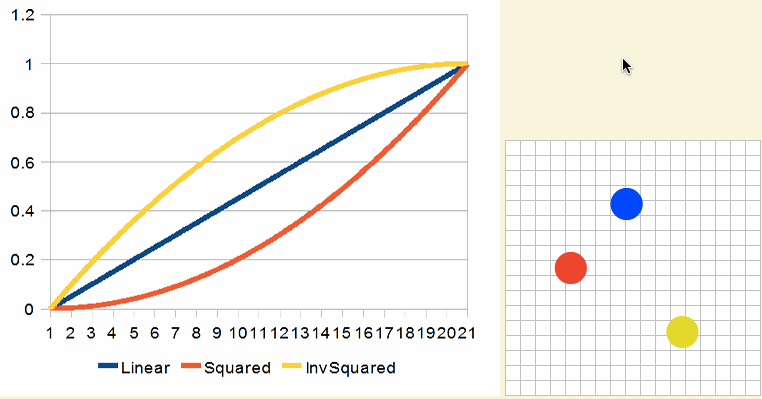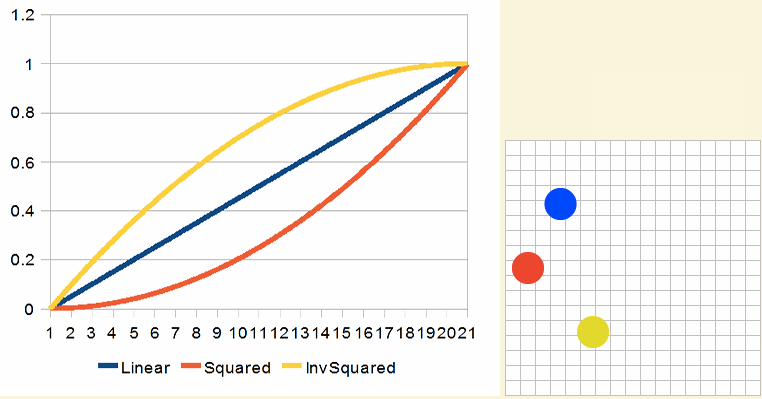
高次幂提高后的立方曲线（Cubed Curves)效果看起来像这样：

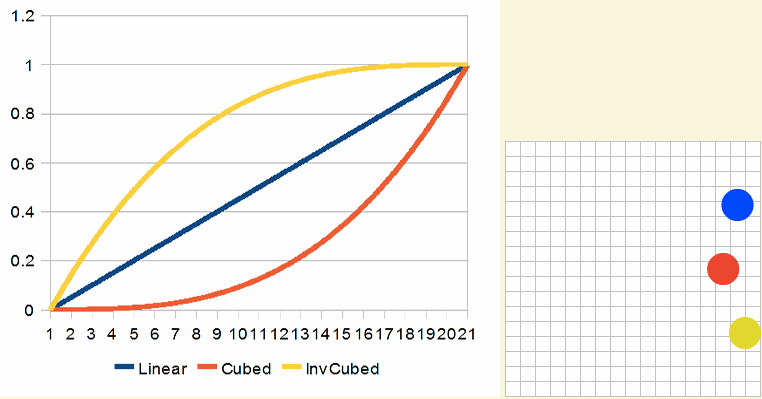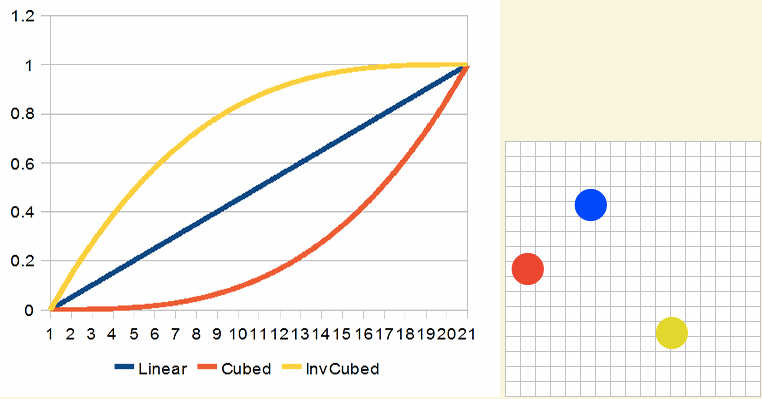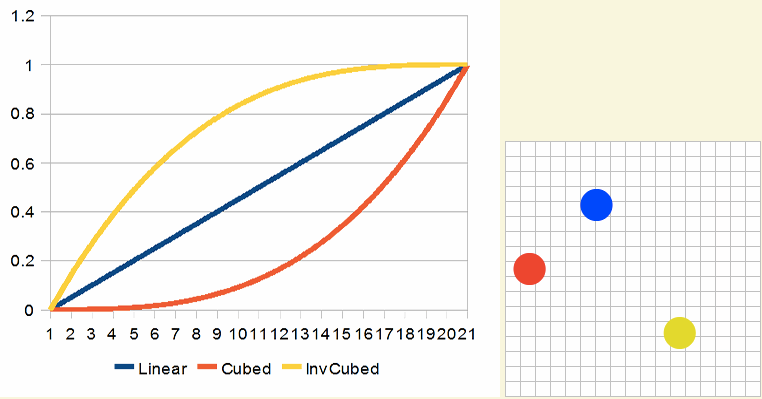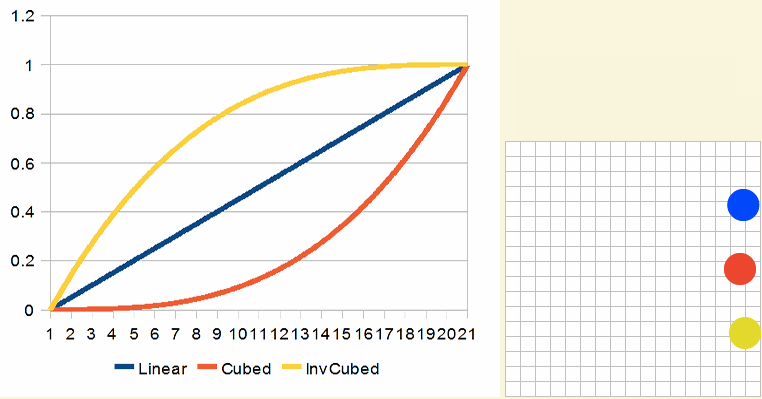
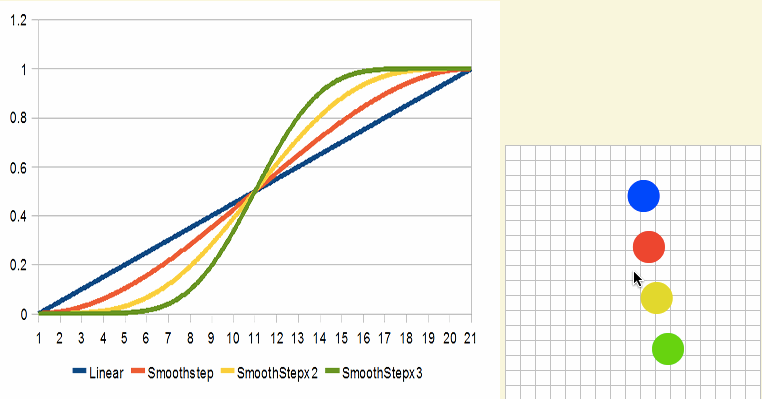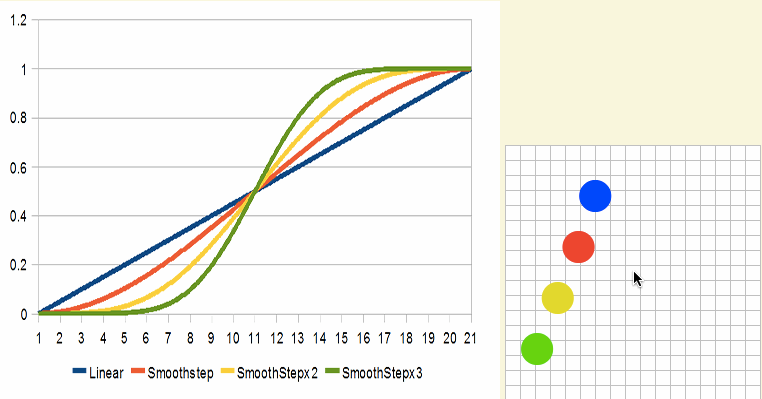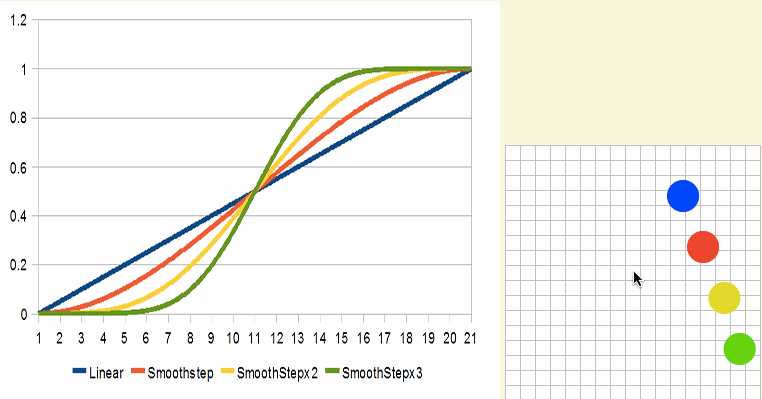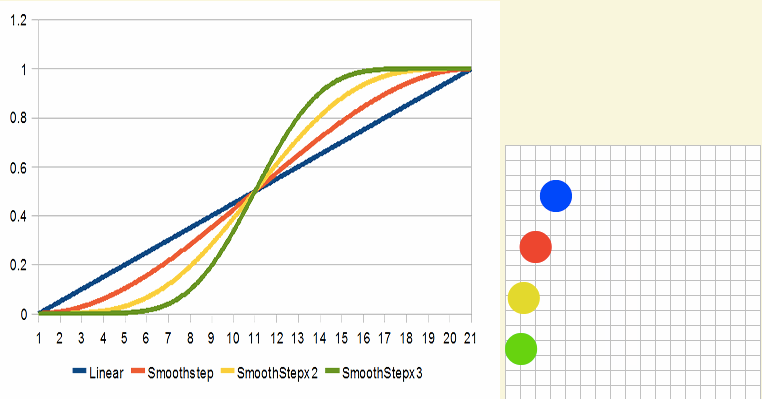
同样的概念也适用于soothstep。比如下图是smoothstep2x和smoothstep3x的效果：

正弦

正弦插值和次幂函数近似：

for (var i = 0; i < n; i++) {
    v = i / n;
    v = sin(v * Math.PI / 2);
    x = (A * v) + (B * (1 - v));
}

反向后更像次幂函数，结果看起来像这样：

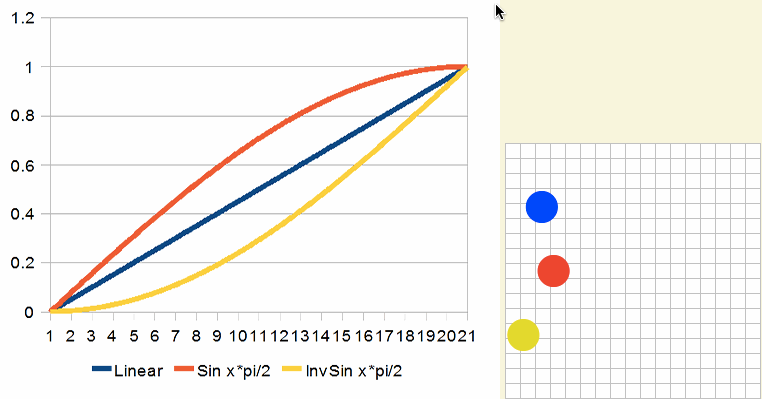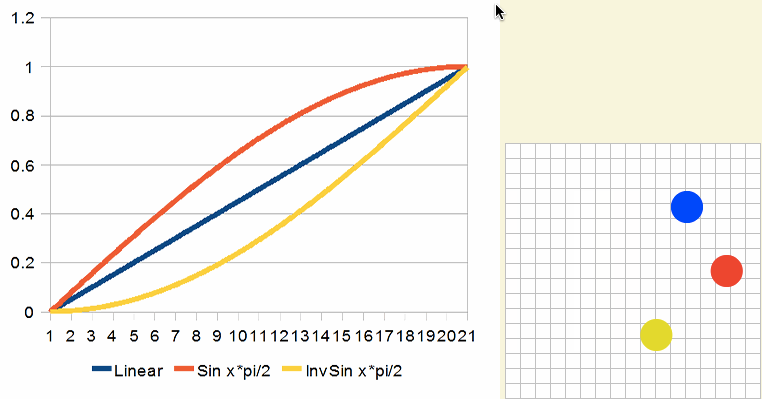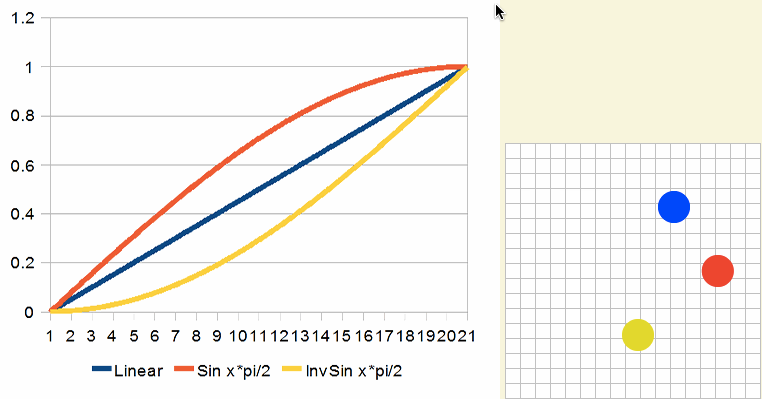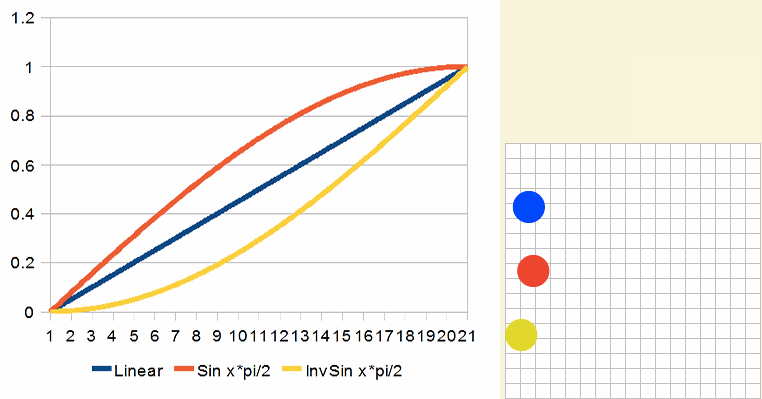
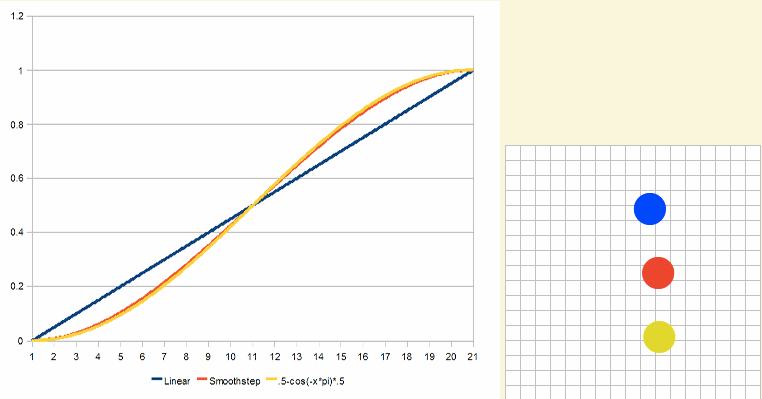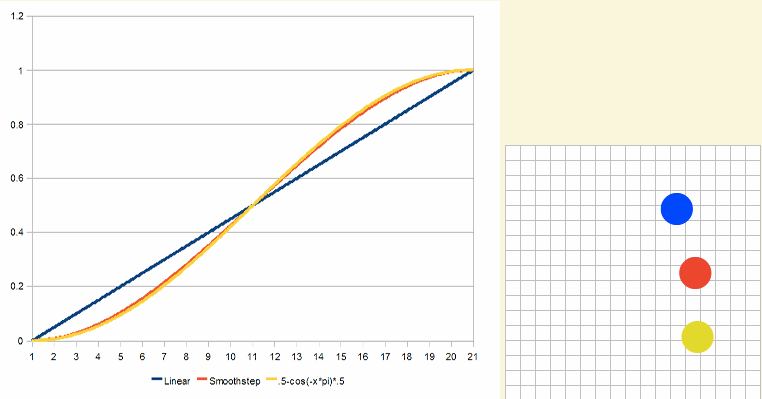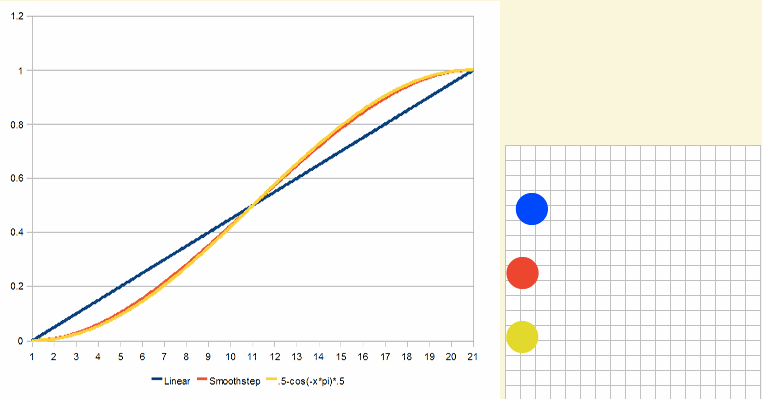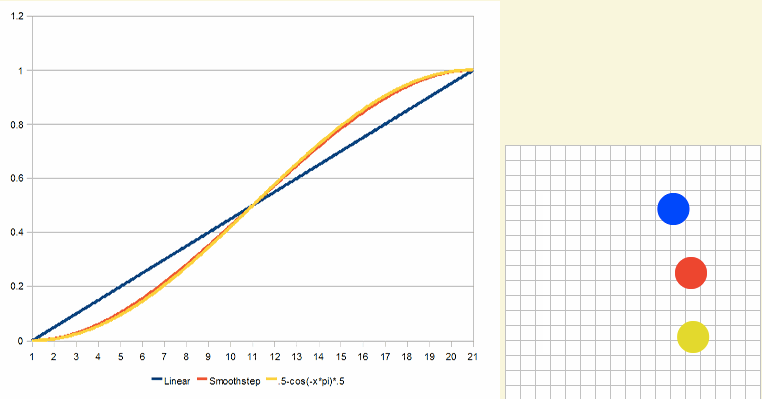
如何使用整条曲线，那么将更接近smoothstep。但性能会更打折扣：

for(var i = 0; i < n; i++) {
    v = i / n;
    v = .5 - cos(-v * Math.PI) * .5;
    X = (A * v) + (B * (1 - v));
}

效果看起来如下：

加权平均数

非常方便的算法，特别是当你无法预知未来目标行为时（比如摄像机跟随目标角色，而角色的位置是一直在改变的）。

v = ((v * (n - 1)) + w) / n;

其中v代表当前值，w代表目标点，n是缓因子，n值越大，v接近w就越慢：

样条

样条函数支持你控制更多的插值点，也就是说你可以让运动轨迹更多样化。

function catmullrom(t, p0, p1, p2, p3){
    return 0.5 * (
        (2 * p1) +
        (-p0 + p2) * t +
        (2 * p0 - 5 * p1 + 4 * p2 - p3) * t * t +
        (-p0 + 3 * p1 - 3 * p2 + p3) * t * t * t
    );
}

效果看起来像下面这样：

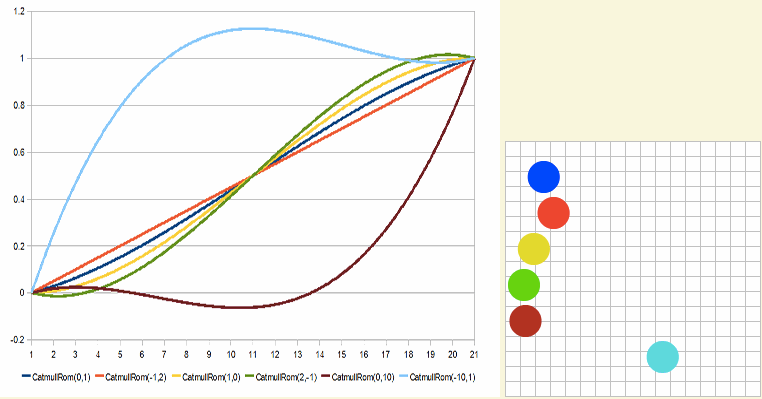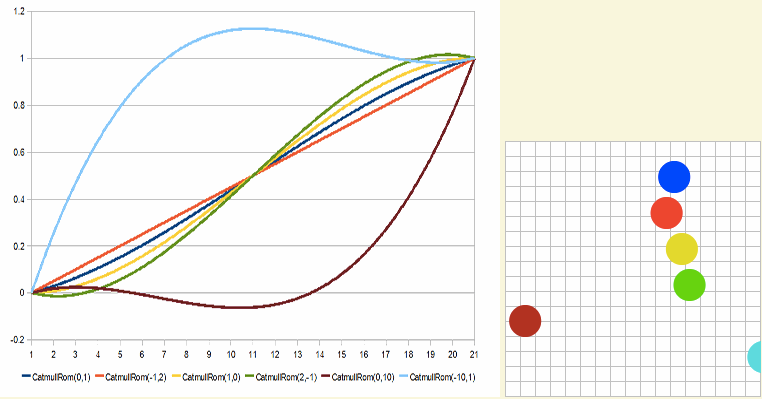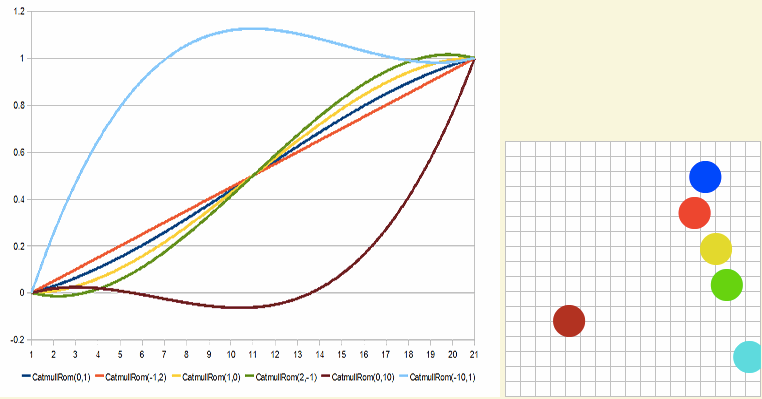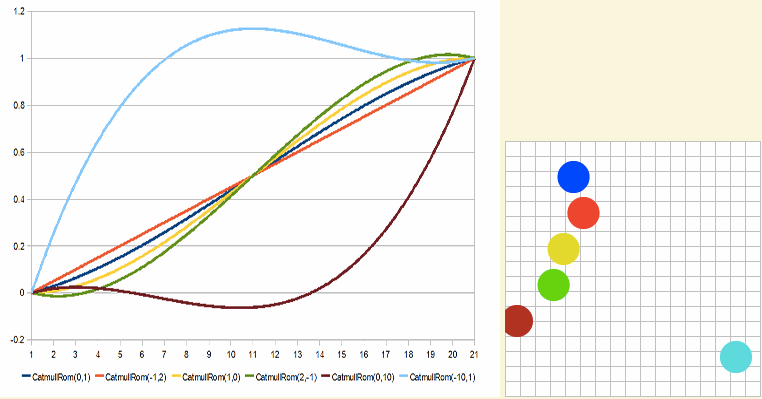
有关于这方面的详细介绍可以阅读《Interpolation Tricks》一文。更多相关的介绍可以阅读下面的文章：

• Quadratic/Cubic versus Linear Interpolations by Alain Brobecker
• Interpolation Methods by Paul Bourke
• Tweener transition types cheat sheet
• Hermite Curve Interpolation by Nils Pipenbrinck
• Tweening by Robert Penner (PDF link)
• Easing Equations by Robert Penner

线性插值如何工作

文章一直提到过：lerp是两点之间的线性插值的别称。它可以改善我们的动画效果，如果你将一个对象从点A移动到点B。

也就是说，如果你有一个对象的当前位置和目标的位置，可以线性内插这些点之间的距离的百分比，并在每个动画帧上更新该位置。

function lerp(position, targetPosition) {
    // 计算当前位置与目标位置差值的`20%`
    // 其中`20%`就是我们的缓动因子
    position.x += (targetPosition.x - position.x) * .2;
    position.y += (targetPosition.y - position.y) * .2;
}

通过这样做，对象移动的量随着位置和目标之间的距离减小而变小。这意味着对象将越来越接近它的目标，速度将减慢，这创造一个很好的缓动效果。

说了这么多理论性的东西，看起来云里来雾里去，那咱们来看看实例中的运用，可能感觉会更好点。

下面这个示例是一个球跟随用户的鼠标或触摸运动的例子。如果我们使用球移动到鼠标移动的地方，球的移动可以非常快但看起来有点脱节。如果我们快速移动鼠标，我们可以看到单独的“球影”。

上面的效果是没有使用lerp，下面的示例添加lerp。下面的效果在你移动鼠标时球不会立即向右移动到鼠标位置，而会每次将它移动10%的距离。

注意球的运动很平滑，整体更令人愉快的效果。

运动中的动画

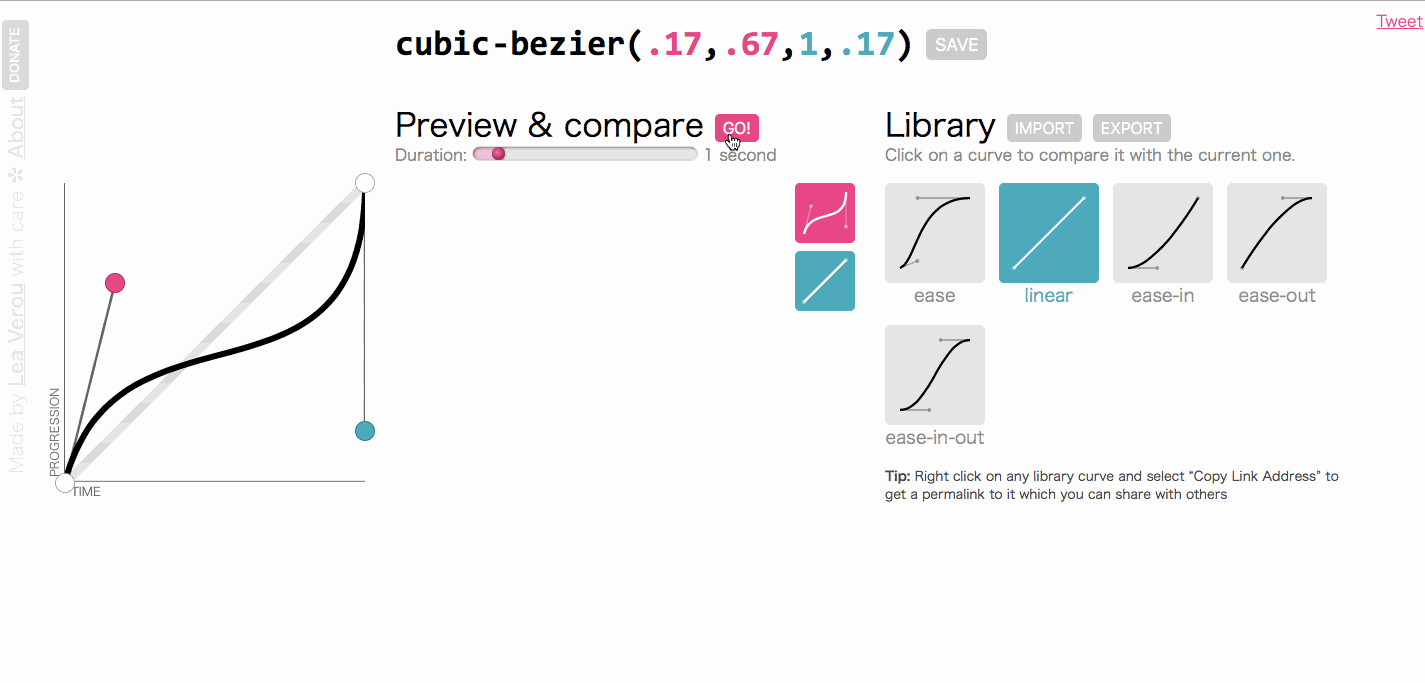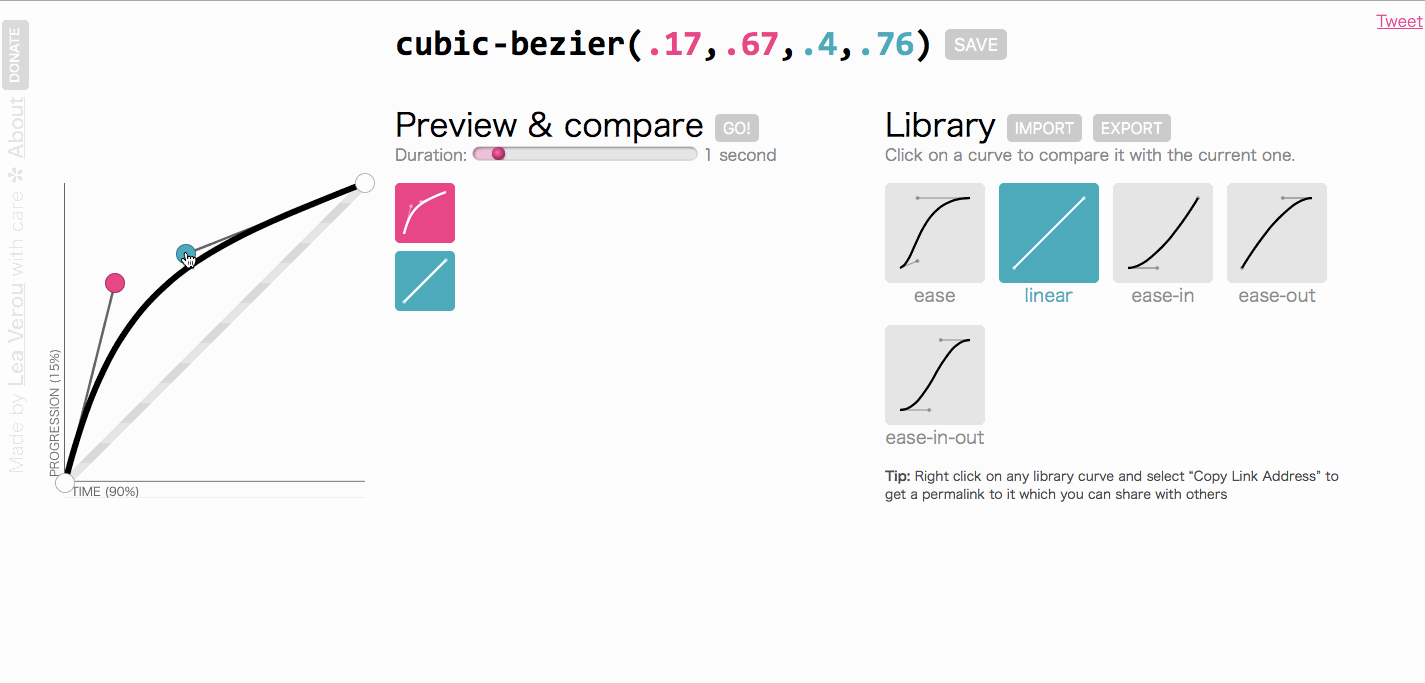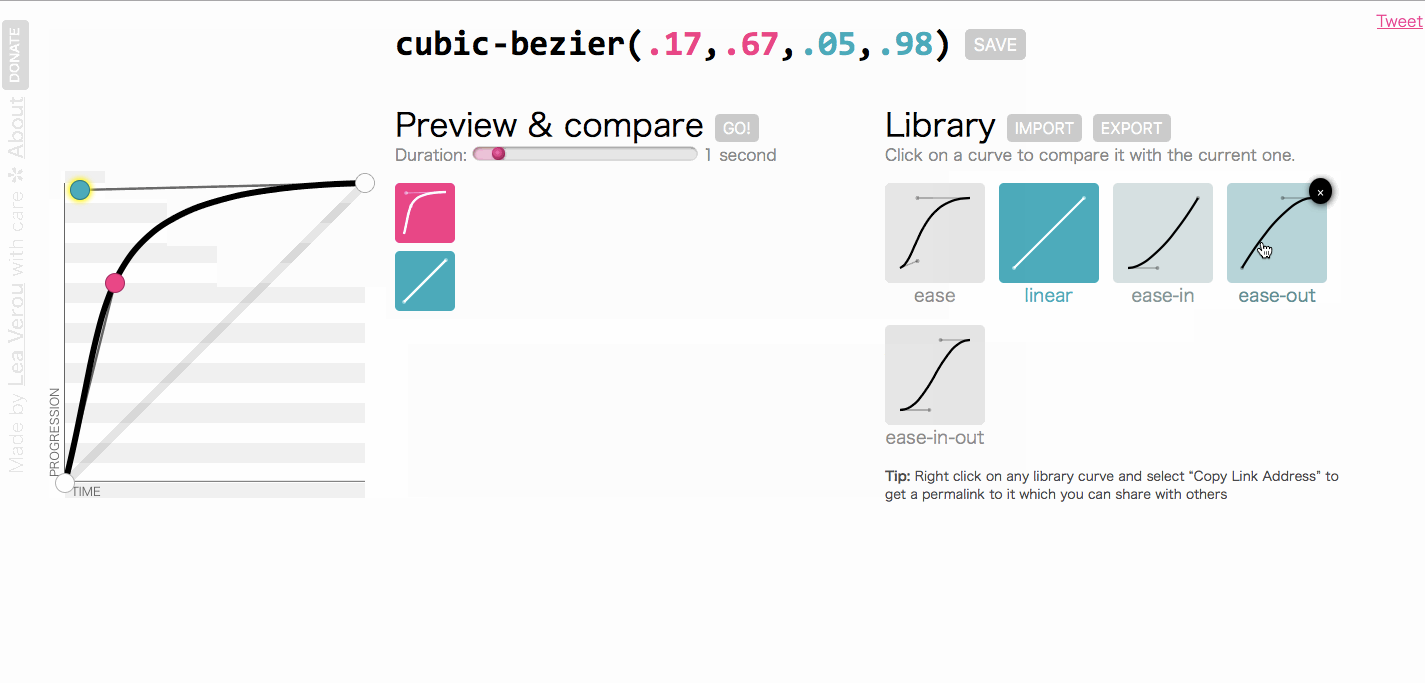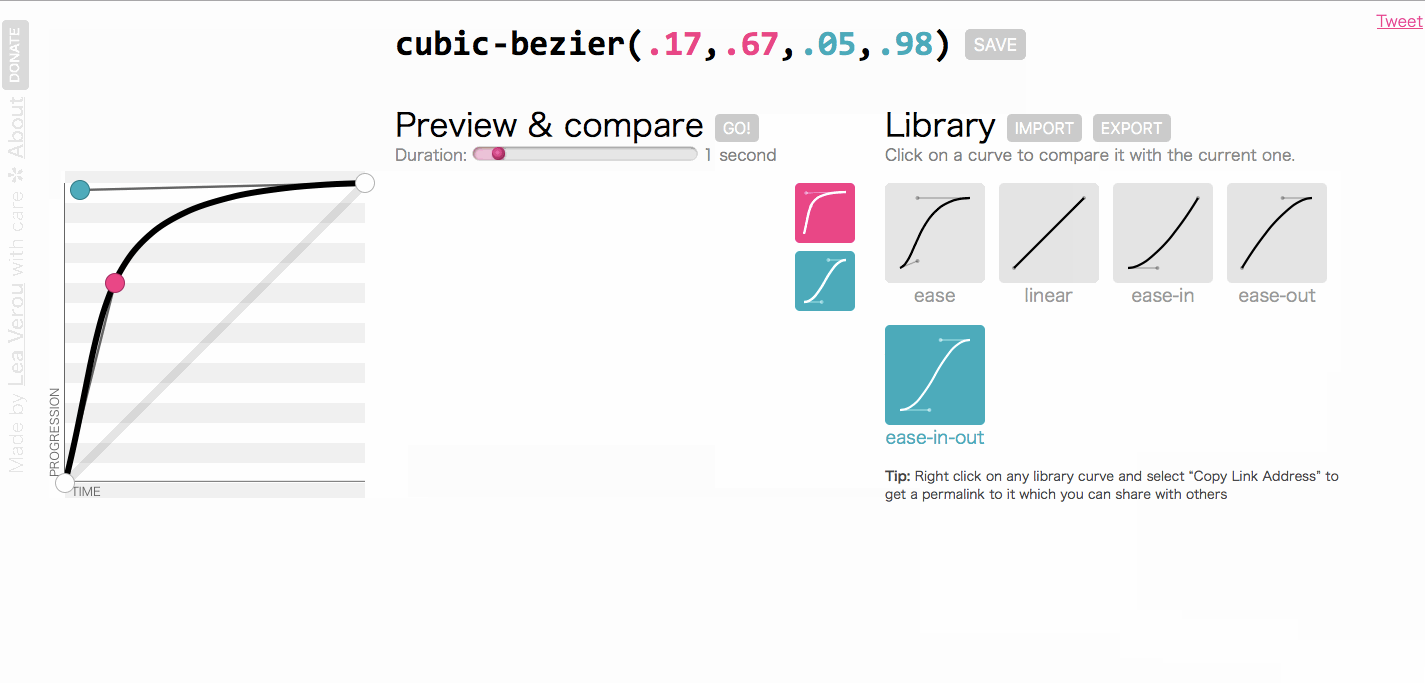
大家对上图应该并不陌生吧。上图是一个cubic-bezier的在线工具**cubic-bezier.com**。这个工具简单绘制需要形状的曲线，然后选择线性曲线作为参考，就可以查看方块的运动变化情况。这其实就是动画中的运动曲线。

我们的主题是聊线性插值，为会会提运动曲线呢？仔细看。我们都知道时间是一秒一秒过去的，也就是线性的，匀速前进的。如果属性值从起始值到结束值是匀速变化的话，那么整个动画看起来就是慢慢地均匀地变化着。但是，如果我们想让动画变得很快或者变得很慢怎么办？答案是我们可以通过“篡改时间”来完成这个任务。实际上就是一条函数曲线。

如下图所示，x轴表示时间的比率，y轴表示属性值。假设属性值从0变化到1，默认情况下线性插值器就和曲线y = x一样，在时间t的位置上的值为f(t) = t 。但是，当我们设置函数y = x ^ 2或者y = x ^ (0.5)时，动画的效果就截然不同。在t = 0.5时，y = x ^ 2 = 0.25 < 0.5，表示它将时间推迟了；而y =x ^ (0.5) = 0.71 > 0.5，表示它将时间提前了。

此外，仔细观察曲线的斜率不难发现，曲线y = x ^ 2的斜率在不断增加，说明变化越来越快，作用在对象上就是刚开始慢，然后不断加速的效果；而曲线y = x ^ (0.5)的斜率在不断减小，说明变化越来越慢，作用在对象上就是开始快，然后不断减速的效果。

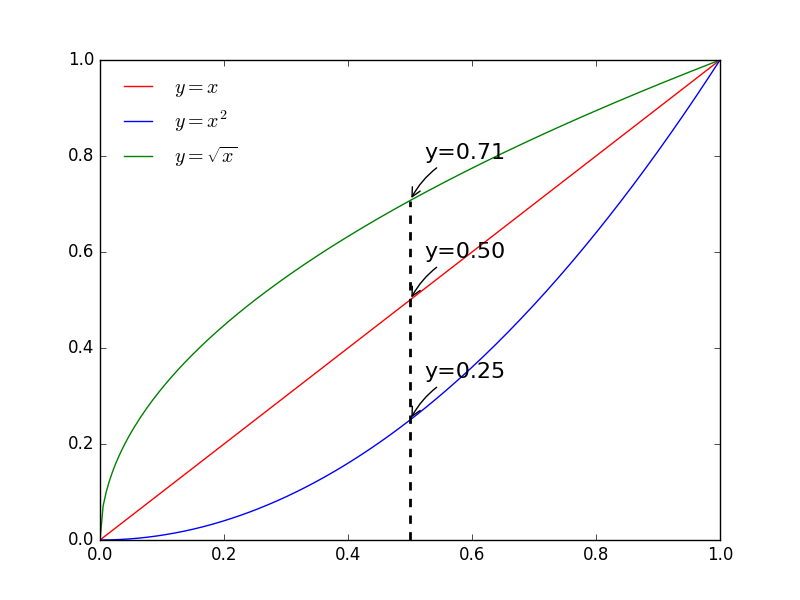
大家或许也发现了，上图的效果和前面介绍的高幂线性插值有点类似。

其实看到这里也有人会问，动画中的那个cubic-bezier值好像只有两个点，那是因为动画贝塞尔曲线的起点和终点已经固定了，分别是(0, 0)和(1, 1)。

cubic-bezier公式不是简单的y = x公式，而是引入了第三个变量t，由于动画中关键在于计算比例，即在总时间的某个时间点百分比得到相应的值相对于最终值的比例，那么只需要得到0 ~ 1区间的曲线即可，而[x, y] => [0, 1]内的曲线则是通过t在0 ~ 1内连续变化而得到：

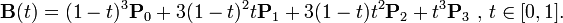
其中P0、P1、P2、P3都为两维xy向量。

有关于贝塞尔曲线的详细介绍，可以阅读前面整理的文章《Canvas学习：贝塞尔曲线》。

从前面的知识中我们了解到，cubic_bezier曲线限制了首尾两控制点的位置，通过调整中间两控制点的位置可以灵活得到常用的动画效果。动画所做的事情就是把x轴当做时间比例，根据曲线得到y轴对应的值，并更新到动画对象中去。比如我们常看到的linear效果：

function linearTween(t, start, end) {
    return t * start + (1 - t) * end;
}

大家或许对easing.js效果并不陌生，里面通过计算得到类似上面linear这样的缓动函数。从而指定动画效果在执行时的速度，使其看起来更加真实。

话又说回来，通过对线性插值的深入理解，回过头来再来理解贝塞尔曲线和缓动函数应该会变得更为简单。除此之外，在很多动画示例中都将会看到lerp函数这个身影，特别是在一些游戏的动效中，因为有它会让你的效果看上去更为细滑。

总结

这篇文章对线性插值的基础知识进行科普。从上面的内容我们可以得知，线性插值lerp最大的特性是能帮助我们在制作动效的时候，会让我们的动效变得更为细滑、流畅。事实也是如此，在很多动画效果中都有lerp的身影。当然，这里介绍的只是lerp的基础知识，它里面还有很多更为有意义的特性，或者说在此基础上能演变出更为强大的特性。但我对这方面了解的比较少，如果你在这方面有深入的了解，欢迎在下面的评论中与我们一起分享。

大漠

常用昵称“大漠”，W3CPlus创始人，目前就职于手淘。对HTML5、CSS3和Sass等前端脚本语言有非常深入的认识和丰富的实践经验，尤其专注对CSS3的研究，是国内最早研究和使用CSS3技术的一批人。CSS3、Sass和Drupal中国布道者。2014年出版《图解CSS3：核心技术与案例实战》。

如需转载，烦请注明出处：https://www.fedev.cn/canvas/interpolation.htmlNike Shox Deliver