Canvas学习：绘制正多边形

发布于大漠

7 年前

到目前为止，我们了解了如何在Canvas中绘制线段、矩形、圆或圆弧线和贝塞尔曲线等。这些都是Canvas的CanvasRenderingContext2D对象自身提供绘制基本图形。但是，我们肯定需要在Canvas中绘制除此之外的其他图形，比如前面所说的绘制箭头或者说我们今天要聊的绘制正多边形。

正多边形

维基百科上是这样描述的：正多边形是所有角都相等、并且所有边都相等的简单多边形，简单多边形是指在任何位置都不与自身相交的多边形。

正多边形的特性

正n边形每个内角为(1 - 2 / n) * 180或者表示为(n - 2) * 180 / n角度。也可以用弧度表示为(n - 2) * π / n 或者(n - 2) / 2n。

正多边形的所有顶点都在同一个外接圆上，每个正多边形都有一个外接圆，这也称为圆内接正多边形。

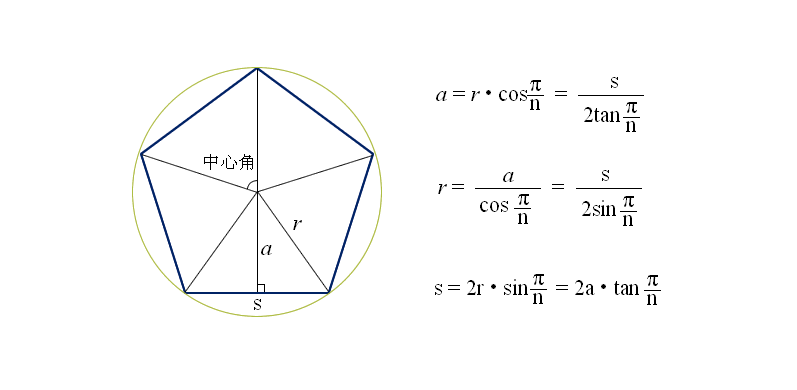
把一个圆分成相等的一些弧，就可以得到这个圆的内接正多边形（Regular Polygon），这个圆就是正多边形的外接圆。外接圆的圆心叫做这个正多边形的中心，外接圆的半径叫做正多边形的半径（Radius），正多边形每一边所对的圆心角叫做正多边形的中心角（圆心角，Central Angle），中心到正多边形的一边的距离叫做正多边形的边心距（Apothem）。

一个圆的圆周是2π，当边的数目为n时，每一个中心角都是2π / n。半径r、边心距a、边长s 都存在着固定的关系，已知其中的两个，都可由上面的公式求出第三个。

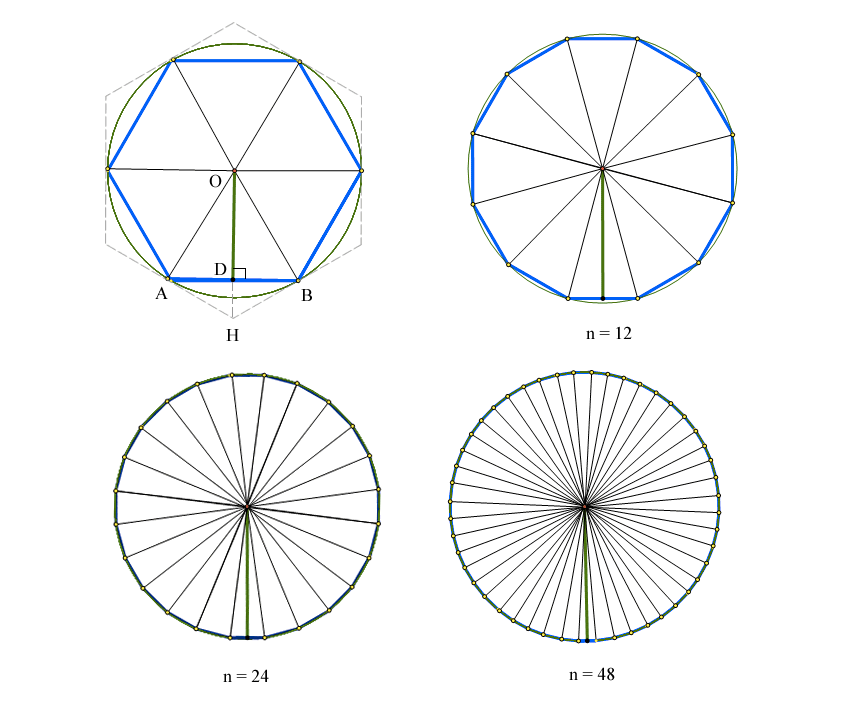
当n接近48这个值时，那这个正多边形也就接近是一个圆了。如下图所示：

正多边形属性

先上张图：

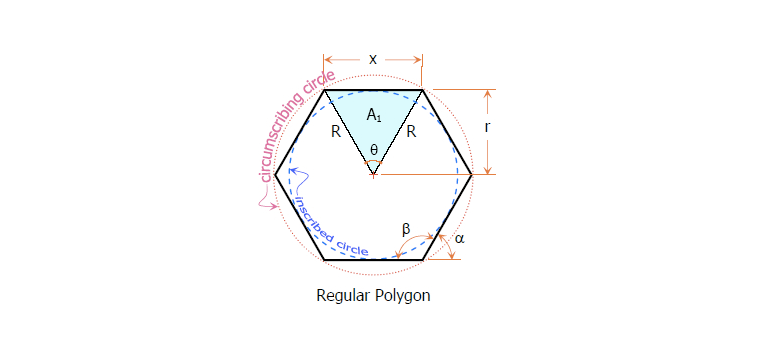
上图描述了正多边形的相关属性：

正多边形的中心点正好是一个正多边形的外接圆的圆心
正多边形每条边的长度都相等，如上图中的x
正多边形的每个内角都相等，如上图中的β
正多边形的每个外角都相等，如上图中的α
正多边形的中心角都相等，如上图中的θ
正多边形的中心点距正多边形的内切圆的半行为r
正多边形的顶点数和边数相等，常用n表示
正多边形中心距正多边形的外接圆（或者正多边中心点距正多边形的顶点）就是正多边形外接圆半么，如上图中的R
正多边形中心点距和每条边的端点构成一个等腰三角形，如上图中的A1。这个三角形的两条边长度相等，刚好是正多边形外接圆半径R，而这个三角形的高，刚好是正多边形内切圆半径r

那么在Canvas中要使用CanvasRenderingContext2D对象自带的方法，比如moveTo()和lineTo()绘制多边形，我们就必须知道正多边形属性之间的关系。也就是这些属性之间的三角函数。言外之意，在Canvas中，我们使用**moveTo()和lineTo()方法，再配合一些简单的三角函数，就可以绘制出任意边数的多边形。**

既然绘制正多边形需要一定的三角函数知道，我们在绘制正多边形之前，先了简单的了解一下这方面的基础。

外角（Exterior Angle）

正多边形的外角是正多边形任意边与相邻边延长直线构成的角：

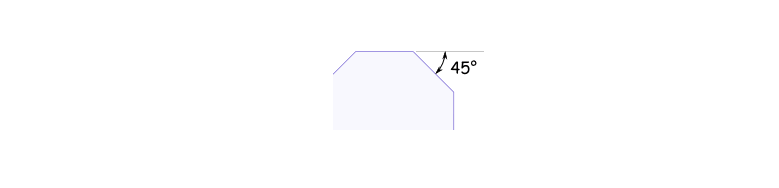
正多边形所有外角之和等于360°。也就是说，每个外角α = 360° / n。比如n=8，一个正八边形，它的外角α = 360° / n = 360° / 8 = 45。

内角（Interior Angles）

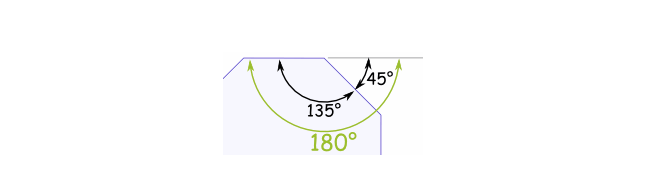
正多边形相邻两条边构成的夹角就是正多边形的一个内角。每个内角都有其相邻的一个外角，它们构成一条直线，也就是说内角加上外角，刚好是180°。也就是内角β = 180° - α。即：β = 180° - 360° /n。上面的公式可以转化为：

β = 180° - 360° / n
  = (n × 180° / n) − (2 × 180° / n)
  = (n − 2) × 180° / n

同样的拿n = 8的正八边形为例：β = (n - 2) × 180° / n = (8 - 2) × 180° / 8，即β = 135°。

中心角

正多边形的中心点与正多边形顶点构成的角，即正多边形每条边对应的夹角称为正多边形的中心角θ。如果正边形有n条边，那么就有n个中心角θ，这样一来θ = 360° / n。

正多边形每个顶点的坐标

通过前面的介绍，我们可以很容易得到正多边形的中心角θ。但在Canvas中要绘制一个正多边形，需要知道正多边形每个顶点的坐标。而这个坐标(xPos, yPos)可以通过三角函数得到。

xPos = cos(θ) * R
yPos = sin(θ) * R

而正多边形所有中心角的和是360°也就是2π，中心角 θ = 2π / n:

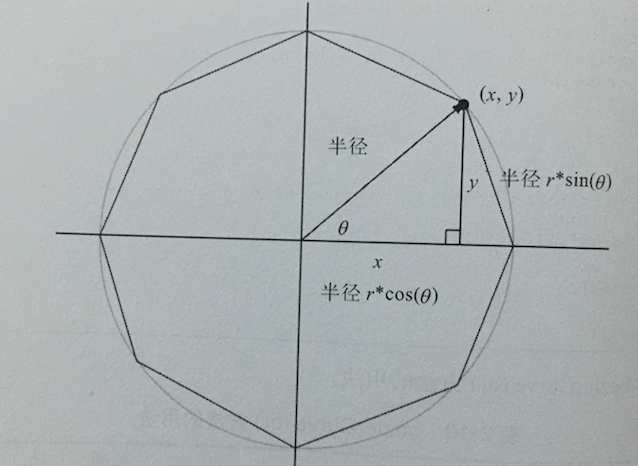
假设我们正多边形的中点心是(xCenter, yCenter)，这样就可以得到每个顶点坐标位置：

xPos = xCenter + Math.cos(angle) * radius;
yPos = yCenter + Math.sin(angle) * radius;

绘制正多边形

前面花了很长的篇幅来介绍正多边形相关知识点。因为只有了解这些基础，才能更好的绘制正多边形，这也是磨刀不误砍柴工。那么我们接下来看怎么绘制一个正多边形。

我们先来看一个简单的绘制方法，比如封装一个绘制正多边形的函数drawPolygons()，给它传几个参数：

ctx：Canvas中绘图环境
num：正边形边数
radius：正边形外接圆半径
arc：是否显示正多边形的外接圆

这样我们就可以撸码了：

function drawPolygons(ctx, num, radius, arc) {
    // 先清Canvas画布，w为Canvas宽度，h为Canvas高度
    ctx.clearRect(-w / 2, -h / 2, w, h);

    ctx.save();
    ctx.beginPath();
    // 通过moveTo绘制移到正多边形起始点
    ctx.moveTo(0, -radius);

    for (var i = 0; i < num; i++) {
        angle = (360 / num) * (i + 1) * Math.PI / 180;
        actAngle = angle - Math.PI / 2;
        x = Math.cos(actAngle) * radius;
        y = Math.sin(actAngle) * radius;
       ctx.lineTo(x, y);
    }
   ctx.closePath();
   ctx.fill();
   ctx.stroke();
        
   // 画外接圆
   if (arc) {
       ctx.beginPath();
       ctx.arc(0, 0, radius, 0, 2 * Math.PI, true);
       ctx.stroke();
   }
}

为了更好的演示，添加几个表单，让我们更好的演示绘制正多边形，比如：

为了让我们绘制正多边形更佳灵活，可以给其传入更多的参数。并且为了绘制边框正多边形和填充正多边形，我们可以多封装两个函数：

// @param {CanvasRenderingContext2D} ctx
// @param {Number} xCenter 中心坐标X点
// @param {Number} yCenter 中心坐标Y点
// @param {Number} radius 外圆半径
// @param {Number} sides 多边形边数
// @param {Number} alpha 角度 默认270度
// @param {Boolean} arc 是否显示外圆
function drawPolygons(ctx, xCenter, yCenter, radius, sides, alpha, arc) {

    var radAngle = Math.PI * 2 / sides;
    var radAlpha = (alpha != 'undefined') ? alpha * Math.PI / 180 : -Math.PI / 2;

    ctx.save();
    ctx.beginPath();

    var xPos = xCenter + Math.cos(radAlpha) * radius;
    var yPos = yCenter + Math.sin(radAlpha) * radius;

    ctx.moveTo(xPos, yPos);

    for (var i = 1; i <= sides; i++) {
        var rad = radAngle * i + radAlpha;
        var xPos = xCenter + Math.cos(rad) * radius;
        var yPos = yCenter + Math.sin(rad) * radius;
        ctx.lineTo(xPos, yPos);
    }

    ctx.closePath();
}

// 绘制填充的多边形
// @param {CanvasRenderingContext2D} ctx
// @param {Number} xCenter 中心点X坐标点
// @param {Number} yCenter 中心点Y坐标点
// @param {Number} radius 外圆半径
// @param {Number} sides 多边形边数
// @param {Number} alpha 角度 默认270度
// @param {Boolean} arc 是否显示外圆
function drawFillPolygon(ctx, xCenter, yCenter, radius, sides, alpha, arc) {
    drawPolygons(ctx, xCenter, yCenter, radius, sides, alpha, arc);
    ctx.fill();

    // 画外接圆
    if (arc) {
        ctx.beginPath();
        ctx.arc(xCenter, yCenter, radius, 0, 2 * Math.PI, true);
        ctx.stroke();
    }
}

// 绘制描边的多边形
// @param {CanvasRenderingContext2D} ctx
// @param {Number} xCenter 中心点X坐标点
// @param {Number} yCenter 中心点Y坐标点
// @param {Number} radius 外圆半径
// @param {Number} sides 多边形边数
// @param {Number} alpha 角度 默认270度
// @param {Boolean} arc 是否显示外圆
function drawStrokePolygon(ctx, xCenter, yCenter, radius, sides, alpha, arc) {
    drawPolygons(ctx, xCenter, yCenter, radius, sides, alpha, arc);
    ctx.stroke();

    // 画外接圆
    if (arc) {
        ctx.beginPath();
        ctx.arc(xCenter, yCenter, radius, 0, 2 * Math.PI, true);
        ctx.stroke();
    }
}

其中还省略了部分代码，全部代码，可以在CodePen上查看：

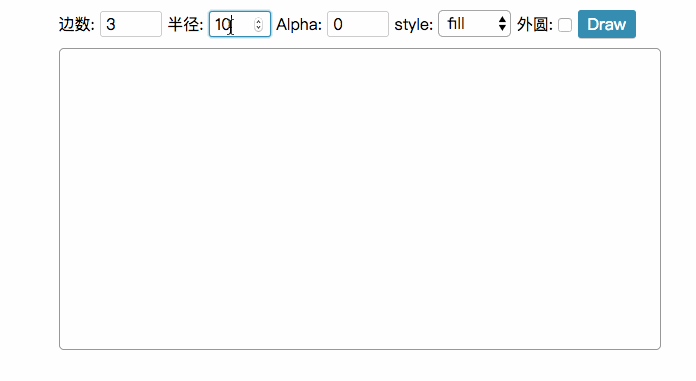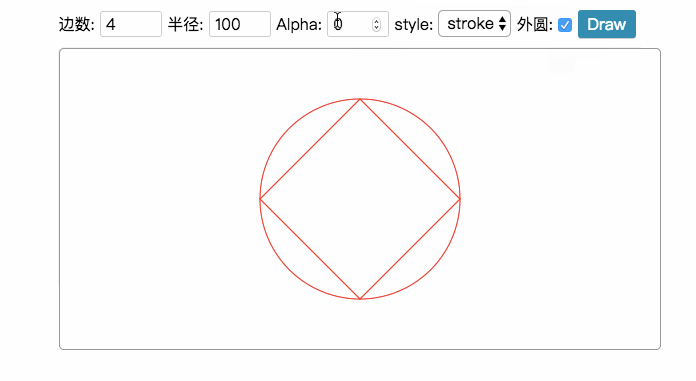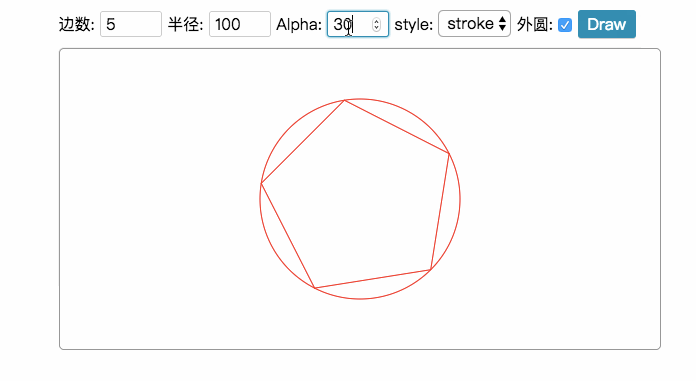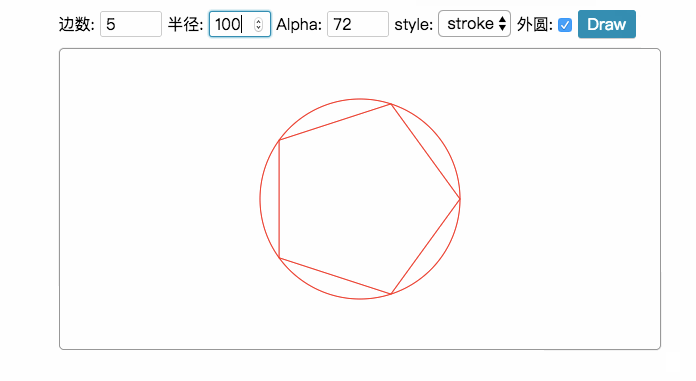
上面我们看到的都是绘制正多边形，但很多时候我们还可以绘制一些星形，比如下面的示例：

// @param {CanvasRenderingContext2D} ctx
// @param {Number} xCenter 中心坐标X点
// @param {Number} yCenter 中心坐标Y点
// @param {Number} radius 外圆半径
// @param {Number} sides 多边形边数
// @param {Number} sideIndent (0 ~ 1)
// @param {Number} alpha 角度 默认270度
// @param {Boolean} arc 是否显示外圆
function drawStarPolygons(ctx, xCenter, yCenter, radius, sides, sideIndent, alpha, arc) {
    var sideIndentRadius = radius * (sideIndent || 0.38);
    var radAngle = alpha ? alpha * Math.PI / 180 : -Math.PI / 2;
    var radAlpha = Math.PI * 2 / sides / 2;

    ctx.save();
    ctx.beginPath();

    var xPos = xCenter + Math.cos(radAngle) * radius;
    var yPos = yCenter + Math.sin(radAngle) * radius;

    ctx.moveTo(xPos, yPos);

    for (var i = 1; i <= sides * 2; i++) {
        var rad = radAlpha * i + radAngle;
        var len = (i % 2) ? sideIndentRadius : radius;
        var xPos = xCenter + Math.cos(rad) * len;
        var yPos = yCenter + Math.sin(rad) * len;

        ctx.lineTo(xPos, yPos);
    }
    ctx.closePath();
}

// 绘制填充的多边形
// @param {CanvasRenderingContext2D} ctx
// @param {Number} xCenter 中心点X坐标点
// @param {Number} yCenter 中心点Y坐标点
// @param {Number} radius 外圆半径
// @param {Number} sides 多边形边数
// @param {Number} sideIndent (0 ~ 1)
// @param {Number} alpha 角度 默认270度
// @param {Boolean} arc 是否显示外圆
function drawFillStarPolygon(ctx, xCenter, yCenter, radius, sides, sideIndent, alpha, arc) {
    drawStarPolygons(ctx, xCenter, yCenter, radius, sides, sideIndent, alpha, arc);
    ctx.fill();

    // 画外接圆
    if (arc) {
        ctx.beginPath();
        ctx.arc(xCenter, yCenter, radius, 0, 2 * Math.PI, true);
        ctx.arc(xCenter, yCenter, radius * sideIndent, 0, 2 * Math.PI, true);
        ctx.stroke();
    }
}

// 绘制描边的多边形
// @param {CanvasRenderingContext2D} ctx
// @param {Number} xCenter 中心点X坐标点
// @param {Number} yCenter 中心点Y坐标点
// @param {Number} radius 外圆半径
// @param {Number} sides 多边形边数
// @param {Number} sideIndent (0 ~ 1)
// @param {Number} alpha 角度 默认270度
// @param {Boolean} arc 是否显示外圆
function drawStrokeStarPolygon(ctx, xCenter, yCenter, radius, sides, sideIndent, alpha, arc) {
    drawStarPolygons(ctx, xCenter, yCenter, radius, sides, sideIndent, alpha, arc);
    ctx.stroke();

    // 画外接圆
    if (arc) {
        ctx.beginPath();
        ctx.arc(xCenter, yCenter, radius, 0, 2 * Math.PI, true);
        ctx.arc(xCenter, yCenter, radius * sideIndent, 0, 2 * Math.PI, true);
        ctx.stroke();
    }
}

总结

这篇文章介绍了如何借助Canvas中的moveTo()和lineTo()方法，再配合一些简单的三角函数的知识绘制正多边形和星形。为了更好的在Canvas中绘制，将其封装成对应的函数。如果你有更好的方法，欢迎在下面的评论中与我们分享。

大漠

常用昵称“大漠”，W3CPlus创始人，目前就职于手淘。对HTML5、CSS3和Sass等前端脚本语言有非常深入的认识和丰富的实践经验，尤其专注对CSS3的研究，是国内最早研究和使用CSS3技术的一批人。CSS3、Sass和Drupal中国布道者。2014年出版《图解CSS3：核心技术与案例实战》。

如需转载，烦请注明出处：https://www.fedev.cn/canvas/drawing-regular-polygons.htmlShop Nike Apparel, Shoes and Accessories