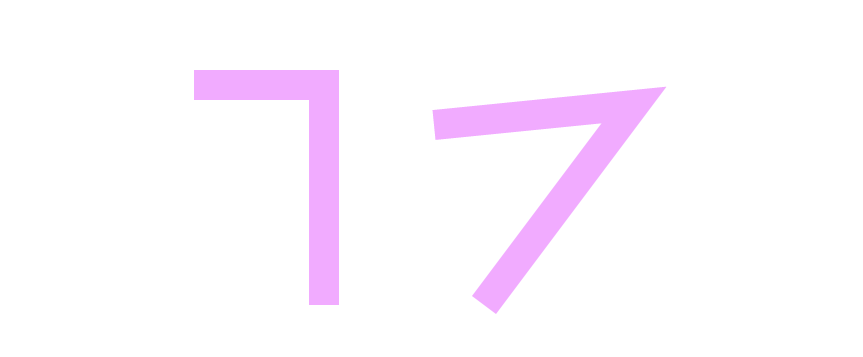Canvas学习:线型
在绘制线段一文中,了解到如何在Canvas中绘制线段。虽然使用Canvas中API可以很轻松的绘制出线段,但里面还是有不少的细节需要了解。这篇文章咱们就来了解线段中的线型。
Canvas中的线型主要包括线宽、线段端点和线段连接点三个部分。那么咱们先来了解线宽。
线宽
通过前面的示例,我们不难发现,在Canvas中通过lineWidth属性来定义线段的粗细。我们可以给其明确指定一个value值,在没有显式设置lineWidth的值时,为以默认值1来确定线段的粗细。
那什么叫线宽呢?在Canvas中,线宽是指给定路径的中心到两边的粗细。换句话说就是在路径的两边各绘制线宽的一半。因为画布的坐标并不和像素直接对应,当需要获得精确的水平或垂直线的时候要特别注意。
想要获得精确的线条,必须对线条是如何绘制出来的有所理解。比如下图,用网格来代表canvas的坐标格,每一格对应屏幕上一个像素点。在左侧图中,填充了(2,1)至5,5的矩形,整个区域的边界刚好落在像素边缘上,这样得到的矩形有着清晰的边缘。如果你想要绘制一条从(3,1)至(3,5),宽度是1.0的线条,就会得到下图中间图一样的结果。实际填充区域(深蓝色部分)仅仅延伸至路径两旁各一半像素,而这半个像素以会以近似的方式进行渲染,这意味着那些像素只是部分着色,结果就是以实际笔触颜色一半色调的颜色来填充整个区域(浅蓝和深蓝的部分)。这就是上例中为何宽度为1.0的线并不准确的原因。要解决这个问题,必须对路径施予更加精确的控制。已经知道1.0的线条会在路径两边各延伸0.5个像素,那么像下图最右侧的那样绘制的线条(从(3.5,1)至(3.5,5)),其边缘正好落在像素边界,填充出来就是准确的宽为1.0的线条。
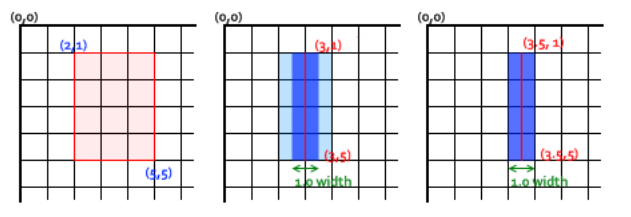
特别注意,在Canvas中绘制
1个像素的线条时,坐标位置需要错开0.5个像素。
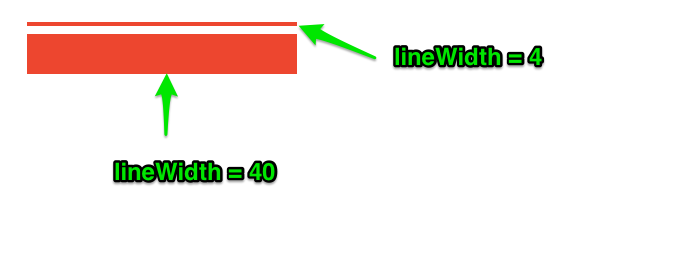
另外在Canvas中绘制路径(线段)时,后面显式设置的lineWidth会覆盖前面的值。比如:
function drawScreen () {
ctx.strokeStyle = "red";
ctx.lineWidth = 4;
ctx.beginPath();
ctx.moveTo(30,30);
ctx.lineTo(300,30);
ctx.stroke();
ctx.lineWidth = 40;
ctx.beginPath();
ctx.moveTo(30,60);
ctx.lineTo(300,60);
ctx.stroke();
}
线段端点
在绘制线段时,可以控制线段端点,这个线段端点也称为线帽。在Canvas的绘图环境中,控制线段端点绘制有一个属性叫CanvasRenderingContext2D.lineCap。
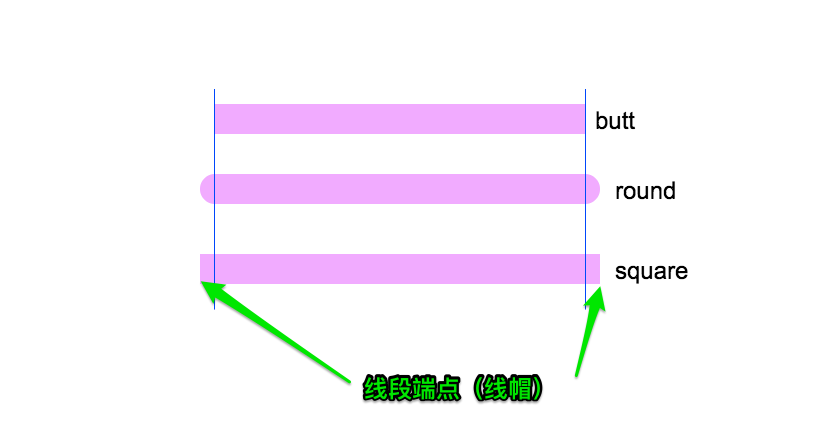
CanvasRenderingContext2D.lineCap有三个值:butt、round和square,其中默认的值是butt。
butt:线段末端以方形结束round:线段末端以圆形结束square:线段末端以方形结束,但是增加了一个宽度和线段相同,高度是线段厚度一半的矩形区域
来看一个小示例:
ctx.lineWidth = 30;
ctx.beginPath();
ctx.lineCap = 'butt';
ctx.moveTo(30,30);
ctx.lineTo(400,30);
ctx.fillText('butt', 410, 40);
ctx.stroke();
ctx.beginPath();
ctx.lineCap = 'round';
ctx.moveTo(30,100);
ctx.lineTo(400,100);
ctx.fillText('round', 430, 110);
ctx.stroke();
ctx.beginPath();
ctx.lineCap = 'square';
ctx.moveTo(30,180);
ctx.lineTo(400,180);
ctx.fillText('square', 430, 190);
ctx.stroke();
上图中,两条蓝色线突出的部分就是在Canvas中所谓的线帽,也就是线段端点。
你可以通过下面的示例,选择表单对应的值,能看到lineCap的效果:
线段连接点
在Canvas中绘制路径(线段),它总有可能会有相连的部分,比如说绘制的一个矩形。那么每两条线段相交的点就是线段的连接点。那么在Canvas中怎么控制线段连接点效果呢?在Canvas中,可以通过CanvasRenderingContext2D.lineJoin来控制。
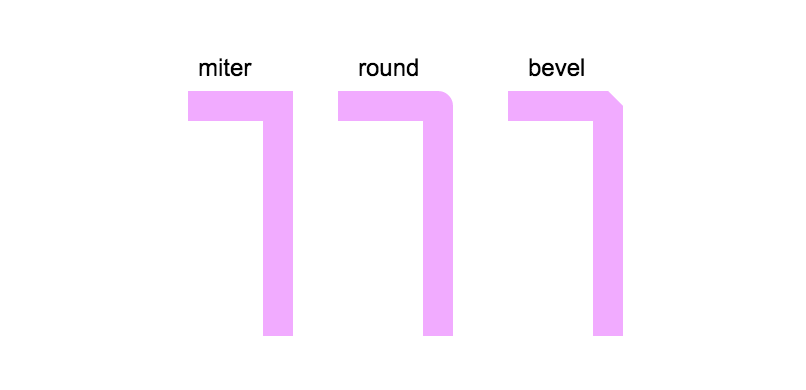
CanvasRenderingContext2D.lineJoin同样有三个值:round、bevel和miter,其中miter是其默认值。
round:通过填充一个额外的,圆心在相连部分末端的扇形,绘制拐角的形状。圆角的半径是线段的宽度bevel:在相连部分的末端填充一个额外的以三角形为底的区域,每个部分都有各自独立的矩形拐角miter:通过延伸相连部分的外边缘,使其相交于一点,形成一个额外的菱形区域。这个设置可以通过miterLimit属性看到效果
来看一个小示例:
function drawScreen () {
ctx.font = "24px Arial";
ctx.strokeStyle = "#f9f";
ctx.lineWidth = 30;
ctx.beginPath();
ctx.lineJoin = 'miter';
ctx.moveTo(30,50);
ctx.lineTo(120,50);
ctx.lineTo(120,280);
ctx.fillText('miter', 40, 20);
ctx.stroke();
ctx.beginPath();
ctx.lineJoin = 'round';
ctx.moveTo(180,50);
ctx.lineTo(280,50);
ctx.lineTo(280,280);
ctx.fillText('round', 200, 20);
ctx.stroke();
ctx.beginPath();
ctx.lineJoin = 'bevel';
ctx.moveTo(350,50);
ctx.lineTo(450,50);
ctx.lineTo(450,280);
ctx.fillText('bevel', 370, 20);
ctx.stroke();
}
lineJoin相对于lineCap要更为复杂一点点。咱们来看下面这张图:
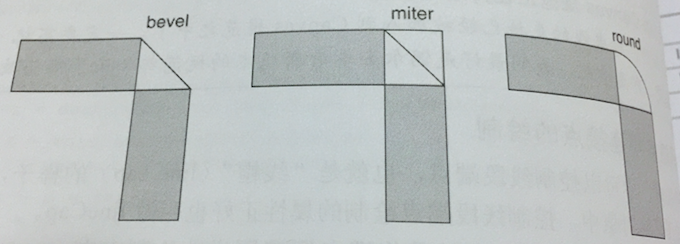
先来看bevel值,两条线段相交的时候,将会用一条直线来连接两个拐角外部的点,使之构成一个三角形。miter的效果和bevel有点类似,只是它还会再画一个三角形,使两个线段的接合处变为一个矩形。而round会使两个线段的拐角处就会画上一段填充好的圆弧。
来看一个动态示例:
只不过取值为miter时,还可以指定一个miterLimit属性,表示连接点(矩形的斜线)计算方式。斜线的长度与二分之一线宽的比值。如下图所示:
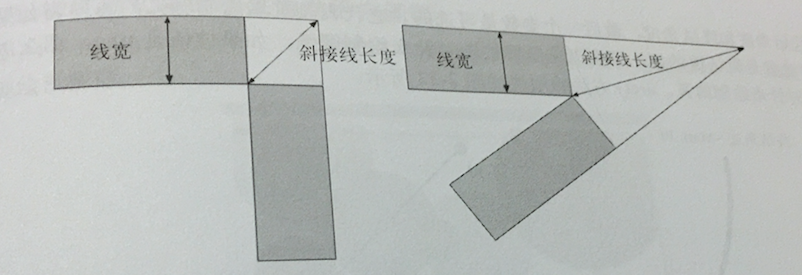
其实这个斜线的长度就是一个直角三角形的边长。
function drawScreen () {
ctx.strokeStyle = "#f9f";
ctx.lineWidth = 30;
ctx.beginPath();
ctx.moveTo(10,60);
ctx.lineTo(140,60);
ctx.lineTo(140,280);
ctx.stroke();
ctx.beginPath();
ctx.moveTo(250,100);
ctx.lineTo(450,80);
ctx.lineTo(300,280);
ctx.stroke();
}
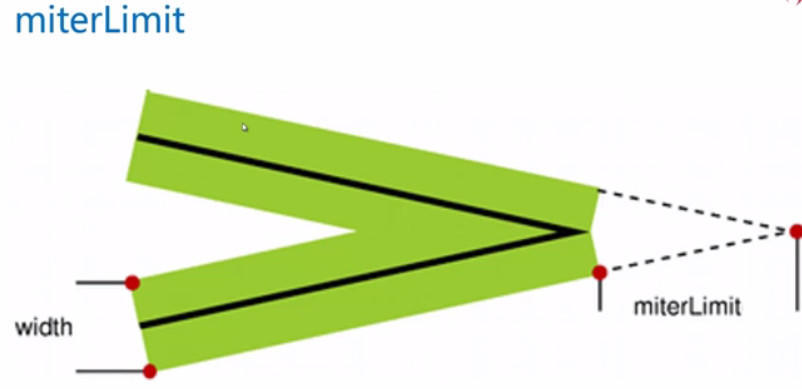
从上面的示例效果中可以看出,如果两个线段夹角很小的话,那么斜线的长度有可能会变得非常长。如果斜线太长,其比值(也就是斜线长度除以二分之一的线宽)就超过了你所指定的miterLimit值,这个时候浏览器就会以bevel的方式来处理两个线段的连接点。
比如,miterLimit默认值为10, 如果2条线相交之后miter的值小于这个miterLimit值, 则 ctx.lineJoin = 'miter' 将自动转换成 ctx.lineJoin = 'bevel'。
小结一下
CanvasRenderingContext2D对象中与线段绘制相关的属性,也就是我们今天所说线型相关的属性:
| 属性 | 描述 | 取值 | 默认值 |
|---|---|---|---|
lineWidth |
设置线段宽度 | 非零的正数 | 1.0 |
lineCap |
控制线段端点如何绘制 | butt、round、square |
butt |
lineJoin |
控制线段连接点如何绘制 | miter、round、bevel |
miter |
miterLimit |
斜线长度与二分之一线宽的比值 | 非零的正数 | 10.0 |
具体的效果:
实例:绘制五角星
最后来安利一个如何使用路径(线段)绘制一个五角星。绘制一个五角星,其最要的是分析五角星的各个顶点的坐标,要得到这五个顶点坐标,要使用到一定的数学知识(其实在Canvas中,数学知识还是很重要的,后面我们会专门来聊这部分内容)。但是浏览器中的坐标系统和数学中的坐标系统有点不一样,具体有何不同,可以阅读前面分享的Cavnas坐标系统一文。
那我们还是回到怎么画五角星这里。在具体绘制五角星之前,先上一张图,这张图能更好的帮助我们分析如何绘制五角星。别的不说,先看图:
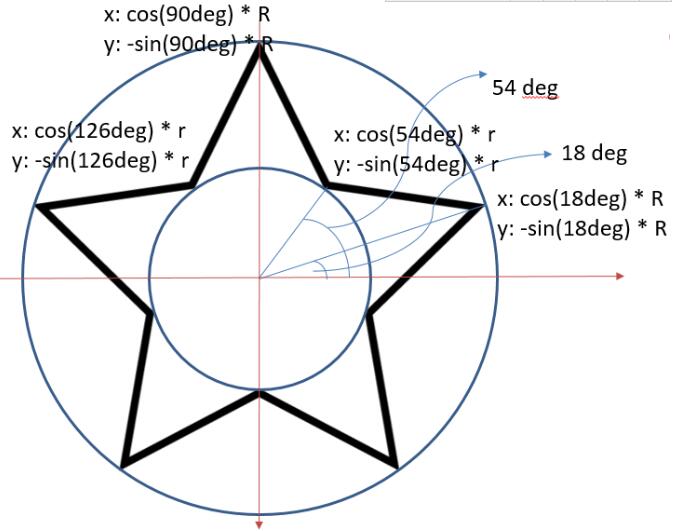
上图已经告诉我们怎么通过数学公式得到五角星的五个坐标点:
- 五角星五个顶点,相连两个顶点之间的夹角为(
360° / 5 = 72°),但浏览器中是使用弧度计算角度的,所以需要将角度转换为弧度:Math.sin(72 / 180) * Math.PI - 五角星由内部一个小圆和外部一个大圆构成
- 以五角星中心为坐标原点,右上角为第一个点,逆时针旋转,外层圆初始角度为
18°,内部小圆初始角度为18°+36°=54° - 不同圆下一个角度都相差
72°
看实例代码:
function drawScreen () {
ctx.strokeStyle = "red";
ctx.lineWidth = 10;
ctx.beginPath();
// i => 五角星五个点
// 100 => 外圆半径
// 50 => 内圆半径
// 200, 100 => 圆心位置
for (var i = 0; i < 5; i++) {
ctx.lineTo(
Math.cos( (18 + 72*i)/180 * Math.PI ) * 100 + 200,
-Math.sin( (18 + 72*i)/180 * Math.PI ) * 100 + 120
);
ctx.lineTo(
Math.cos( (54 + 72*i)/180 * Math.PI ) * 50 + 200,
-Math.sin( (54 + 72*i)/180 * Math.PI ) * 50 + 120
);
}
ctx.closePath();
ctx.stroke();
}
效果如下:
可以将上面的代码封装一下,根据上面的示例,我们可以提取绘制五角星的五个参数:
ctx:Canvas里绘图环境R:大圆半径r:小圆半径x,y:圆心坐标值
将它封装成一个drawStar()函数,并且把这个五个参数传给这个函数:
function drawStar(ctx, x, y, R, r) {
ctx.beginPath();
for (var i = 0; i < 5; i++) {
ctx.lineTo(
Math.cos((18 + i * 72) / 180 * Math.PI) * R + x,
-Math.sin((18 + i * 72) / 180 * Math.PI) * R + y
);
ctx.lineTo(
Math.cos((54 + i * 72) / 180 * Math.PI) * r + x,
-Math.sin((54 + i * 72) / 180 * Math.PI) * r + y
);
}
ctx.closePath();
ctx.stroke();
}
然后在直接调用这个已封装的函数:
function drawScreen () {
ctx.strokeStyle = "red";
ctx.lineWidth = 10;
drawStar(ctx, 200, 120, 100, 50);
}
最终效果是一样的:
到这里,是不是想到可以绘制一面中国国旗的效果,那么还需要一个旋转的功能。
将上面的封装函数,添加一个rotation参数:
function drawStar(ctx, x, y, R, r, rotation = 0) {
ctx.beginPath();
for (var i = 0; i < 5; i++) {
ctx.lineTo(
Math.cos ( (18 + i*72 - rotation) / 180 * Math.PI ) * R + x,
-Math.sin( (18 + i*72 - rotation) / 180 * Math.PI ) * R + y
);
ctx.lineTo(
Math.cos ( (54 + i*72 - rotation) / 180 * Math.PI ) * r + x,
-Math.sin( (54 + i*72 - rotation) / 180 * Math.PI ) * r + y
);
}
ctx.closePath();
ctx.stroke();
}
那具体怎么画出一面中国国旗的效果,自己动手吧。
总结
这篇主要介绍了Canvas中线型的一些属性,比如说通过lineWidth来控制线段的粗线,lineCap来控制线段端点的绘制方式,lineJoin控制线段连接处的绘制方式。最后绘制了一个五角星的实例,当然还提到了绘制国旗,在这个我们用到了一个fillRect(x,y,width,height)的方法,绘制了矩形(当然,我们使用路径也可以绘制一个矩形)。使用这个方法绘制矩形是如此的方便与简单,那么怎么绘制矩形呢?我们将在下一节上来聊。如果感兴趣的话,欢迎持续关注相关更新。
如需转载,烦请注明出处:https://www.fedev.cn/canvas/canvas-line-style.htmlThe 13th Version UA Yeezy Boost 350 Turtle Dove, the perfect version