Canvas粒子系统：3D球体

前些日子在Codepen上看到了一个很惊艳的3D特效，一时惊叹，fork下来后，读了一下作者的源码，200多行，十分精简，但是内劲无穷。这里和大家分享一下作者的思路和一些基础的数学知识，

希望能给大家带来一点思考和启发，先来看一个效果：

动画生成过程

• 创建canvas，设置canvas中心点，变量初始化:function setParameters
• 生成指定数量的例子 同时完成例子的初始化(设置粒子x,y,z 以及增量vx,vy,vz)：function createParticles
• 初始化不同形状:function setupFigure
• 给click(立即切换到下一图形) 和 onmouseover(旋转), 绑定this 因为addEventListener 会把this 绑定在DOM上:function reconstructMethod
• bindEvent 给 click(立即切换到下一图形) 和 onmouseover(旋转) 绑定事件
• 绘图:function drawFigure

其中涉及坐标旋转的代码可以参照之前3D旋转球的博文 有详细说明 这里不做赘述:如何用Canvas做一个3D球

重点 (绘图: drawFigure)

球体制作在之前的博文里提到过，不做赘述.

对于环形制作，看看源码里的环形公式：

createTorus : function(){ var theta = Math.random() * Math.PI * 2, x = this.SCATTER_RADIUS + this.SCATTER_RADIUS / 6 * Math.cos(theta), y = this.SCATTER_RADIUS / 6 * Math.sin(theta), phi = Math.random() * Math.PI * 2;

return {
    x : x * Math.cos(phi),
    y : y,
    z : x * Math.sin(phi),
    hue : Math.round(phi / Math.PI * 30)
};

}

环形 x, y, z 推导 (x屏幕面的x方向， y屏幕面的y方向， z 垂直于屏幕面的方向)

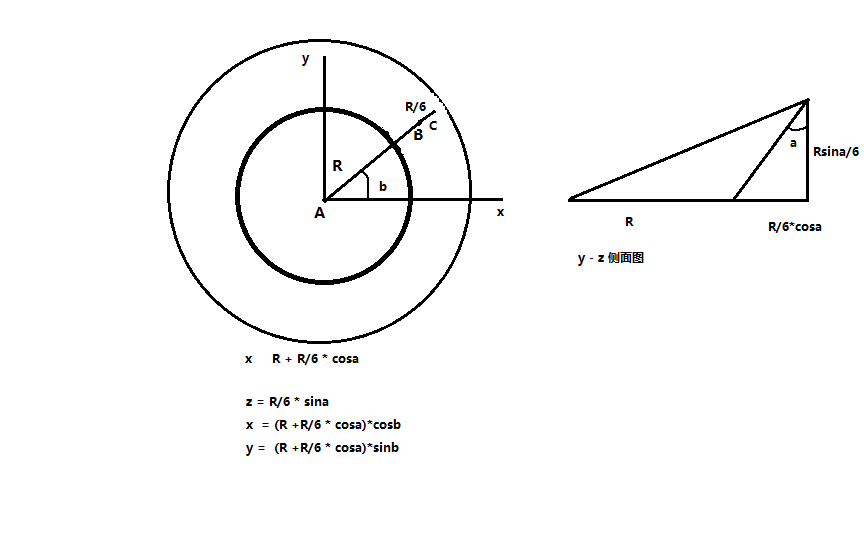
环形的z轴是相对屏幕对称的。

圆锥制作，看看源码里的公式

createCone : function(){
    var status = Math.random() > 1 / 3,
        x,
        y,
        phi = Math.random() * Math.PI * 2,
        rate = Math.tan(30 / 180 * Math.PI) / this.CONE_ASPECT_RATIO;

    if(status){
        y = this.SCATTER_RADIUS * (1 - Math.random() * 2);
        x = (this.SCATTER_RADIUS - y) * rate;
    }else{
        y = -this.SCATTER_RADIUS;
        x = this.SCATTER_RADIUS * 2 * rate * Math.random();
    }
    return {
        x : x * Math.cos(phi),
        y : y,
        z : x * Math.sin(phi),
        hue : Math.round(phi / Math.PI * 30)
    };
},

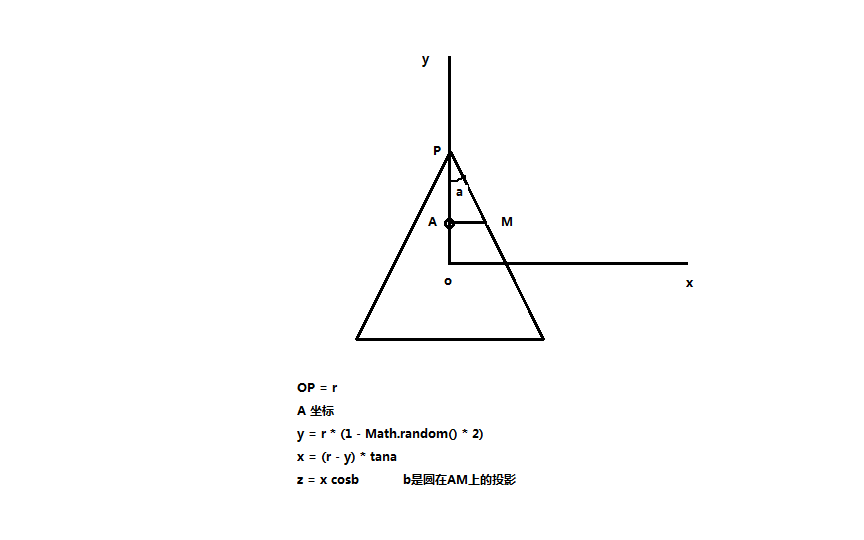
这里 tana 被作者替换成 1.5 tan30， 这里我们可以理解为a 为30，宽高比为1.5。

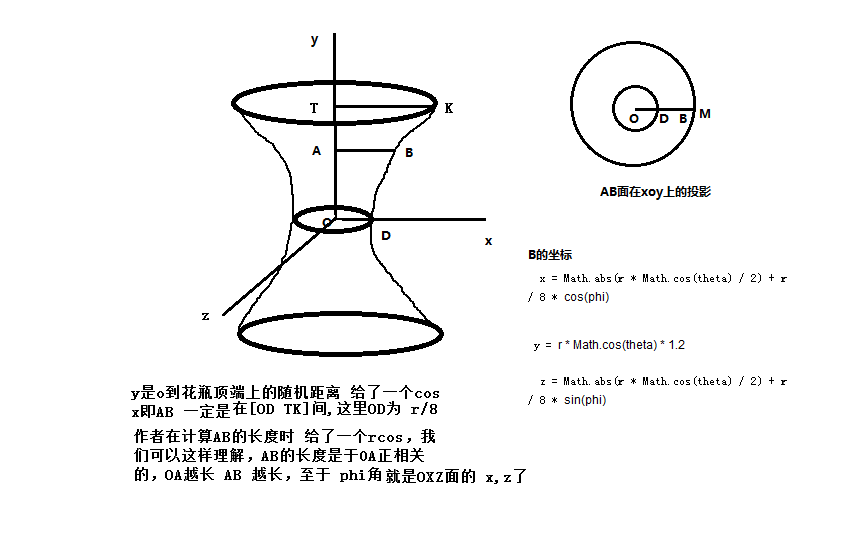
花瓶形(不知道数学里叫什么) 看看源码里的公式

createVase : function(){
    var theta = Math.random() * Math.PI,
        // x = Math.abs(this.SCATTER_RADIUS * Math.cos(theta) / 2) + this.SCATTER_RADIUS / 8,
        x = Math.abs(this.SCATTER_RADIUS * Math.cos(theta) / 2) + this.SCATTER_RADIUS / 8,
        y = this.SCATTER_RADIUS * Math.cos(theta) * 1.2,
        phi = Math.random() * Math.PI * 2;

    return {
        x : x * Math.cos(phi),
        y : y,
        z : x * Math.sin(phi),
        hue : Math.round(phi / Math.PI * 30)
    };
}

结语

Canvas 3D 坐标转换可谓基础，掌握好canvas坐标转换，配合图形的三维方程，可以让粒子做出美妙的运动，释放无穷尽的想象。

Shadow Walker

一名在校研究生，热爱前端，热爱英语，热爱摄影，喜欢一切能表达情绪的东西，喜欢黑色，喜欢秋天，喜欢孤独。。

如需转载，烦请注明出处：https://www.fedev.cn/canvas/deformable-particles.htmlOff White X Max 90