理解动画中的线性插值
在传统(手绘)一个高级动画或者动画艺术家都喜欢绘制关键帧来定义一个动画。

现场传递给助理,一般是实习生或者初级艺术家在此基础上做一些其他性的工作,具体的说,他们就是在关键帧动画之间添加一些中间片段让动画看起来更流畅,更自然。
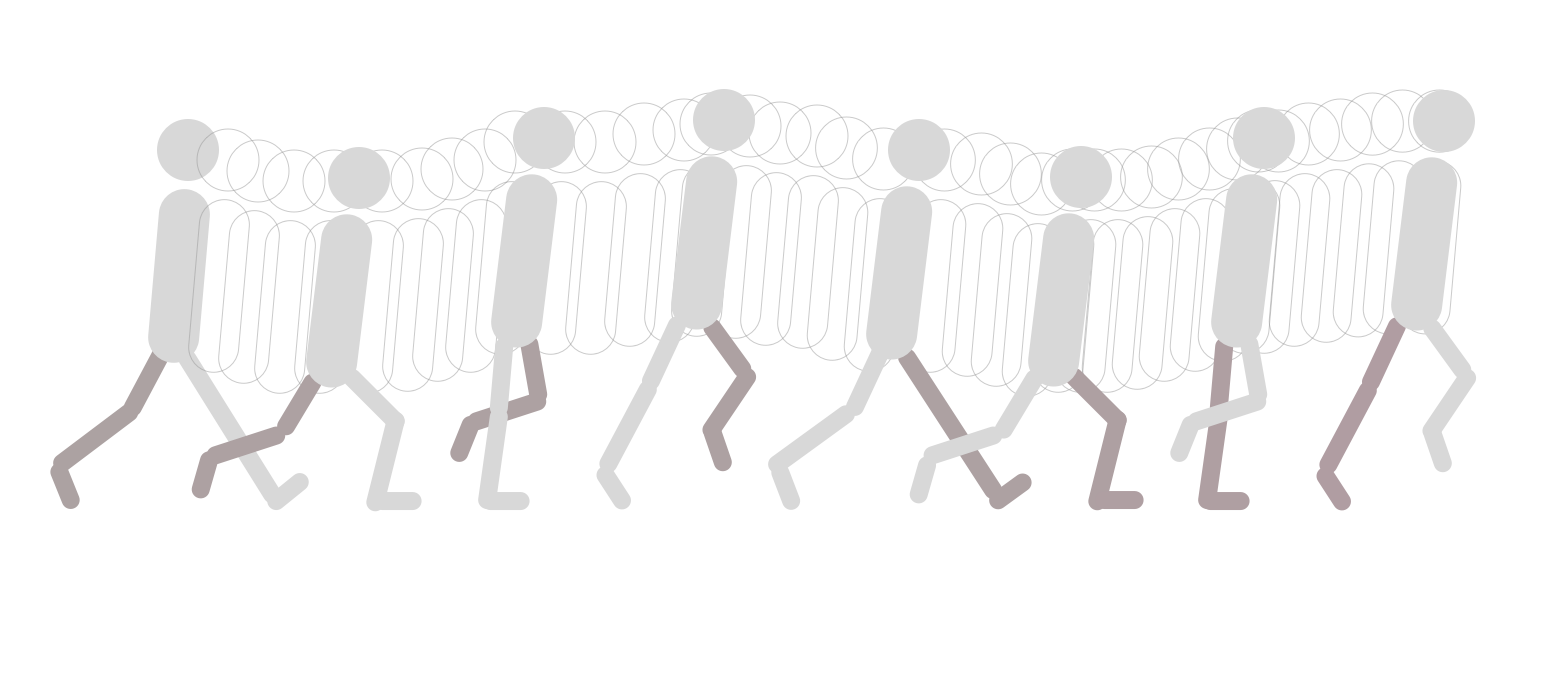
他们可以不考虑或者不讨论动画的中间帧。但绘制动画的中间帧是很有必要的,或者说这方面的工作是繁重的。但这是二十世纪之间的艺术家们做的事情,在今天这些事情都是让计算机来处理这些繁重的任务。
还记得在小学的时候,老师告诉你电脑是笨蛋吗?电脑需要被告知一系列的确切步骤,他们才知道需要做什么。今天我们来看看这一序列的步骤或算法,帮助计算机绘制动画关键帧之间必要的中间画。

我将使用HTML5的Canvas和JavaScript来说明这个算法。即使你都不知道他们,按着下面的步骤来阅读也能理解这篇文章。
目标
我们的目标很简单,就是整一个动画的球,这个球从A点(startX, startY)移动到B点(endX, endY)。

如果这个场景传递给一个传统的工作室,那么高级艺术家将会像下面那样绘制关键的动画帧:

然后初级艺术家们将会在图纸中绘制动画关键帧之间的动画帧:
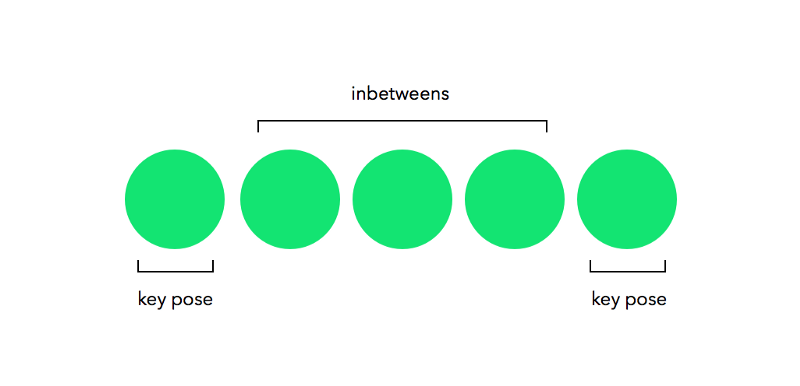
再次提醒大家,没有动画工作室,我们也没有初级的艺术家。我们只有一个目标和一台电脑,我们现在能做的就是写一些正确的代码,用代码来替代初级艺术家们在图纸中绘制工作。
实现方法
我们在技术上需要在HTML中写一行代码:
<canvas id=”canvas”></canvas>
接下来写一些JavaScript代码,下面的JavaScript代码让我们拿到HTML中的<canvas>元素,并且得到一个canvas的2d绘图环境,然后让Canvas画布的大小和视频的大小一致:
const canvas = document.getElementById('canvas');
const context = canvas.getContext('2d');
const width = canvas.width = window.innerWidth;
const height = canvas.height = window.innerHeight;
下面的函数绘制一个绿色的实圆,这个圆的半径为radius,并且其圆心的位置在坐标中的x和y处:
function drawBall(x, y, radius) {
context.beginPath();
context.fillStyle = '#66da79';
context.arc(x, y, radius, 0, Math.PI * 2, false);
context.fill();
}
上面的代码只是画了一个圆的形状,但没有任何动画,只有下面的代码会让你变得更为有趣:
// A点位置
let startX = 50, startY = 50;
// B点位置
let endX = 420, endY = 380;
let x = startX, y = startY;
update();
function update() {
context.clearRect(0, 0, width, height);
drawBall(x, y, 30);
requestAnimationFrame(update);
}
首先,注意上面的update()函数,被称为对其声明,其次,注意requestAnimationFrame(update)表示反复调用update()函数。
这就类似一个翻书的效果,翻书的效果就像创建一个翻转的动画,其创造了一个错觉,前面不断的反复调用update()函数也类似于翻书一样创建一个动画的错觉。

虽然我相信你理解了我要说的意思,但这里还是需要提出**update**这个词。函数可以被称为一切。有些程序员喜欢称之为nextFrame或loop或draw或flip。最重要的是这个函数能做什么。
在后续调用update()函数,我们期望的是这个函数能在canvas画布上绘制一个比前面一个稍微不同的图形。
当前update()函数你可能也已经注意到了,它每次调用drawBall(x, y, 30)只是在相同的位置绘制了一个圆心在(x, y ),半径为30的绿色圆。因此它并没有任何动画效果。
接下来我们来改变这样的现象。每次update()的迭代,给x和y做一个增量的计算,这样就会有一个动画效果:
function update() {
context.clearRect(0, 0, width, height);
drawBall(x, y, 30);
x++;
y++;
requestAnimationFrame(update);
}
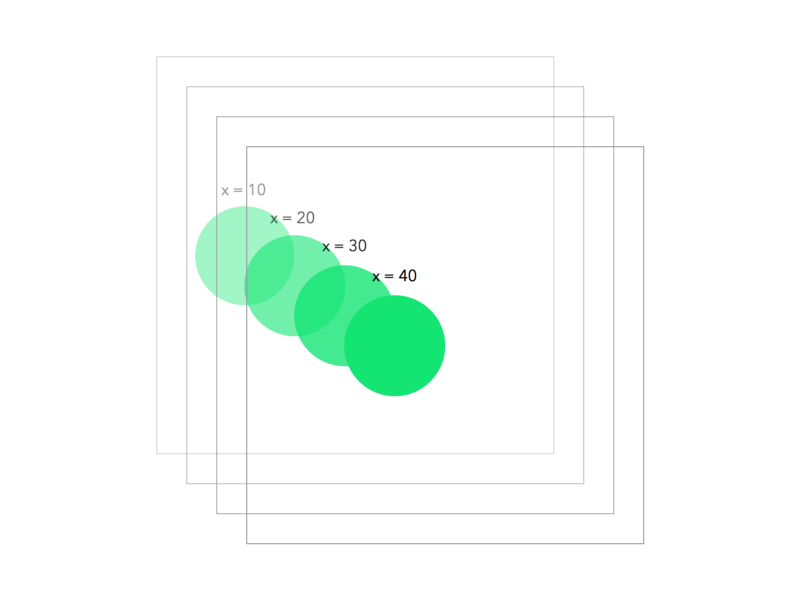
每次迭代,绿色的球会沿着x和y方向向前移动和重复调用update()函数,动画会更新结果,如下图所示:

上面的效果是球会一直向前移,但我们的目标是将球从起始位置移动到结束位置。所以我们需要对球移动到结束位置做一下相关的处理。
最为简单的解决方案就是在小于endX和endY的值做x和y的增值处理。这样球一旦移动的位置超过endX和endY坐标时,绿色的球就停止运动。
function update() {
context.clearRect(0, 0, width, height);
drawBall(x, y, 30);
if (x <= endX && y <= endY) {
x++;
y++;
}
requestAnimationFrame(update);
}
不过在这种方法中有一个错误。你看到了吗?
这里的问题是,让x和y增加值1并不能让球到达任何你想要的最终位置。例如,结束位置是(500, 500),你从(0, 0)开始,x和y依次增量1,最终可以让球到达你想要的结束位置(500, 500),但如果我说结束位置是(432, 373)呢?结果又将如何?
其实上述方法事实上只能让你的终点在一条与水平轴成45度的直线上:
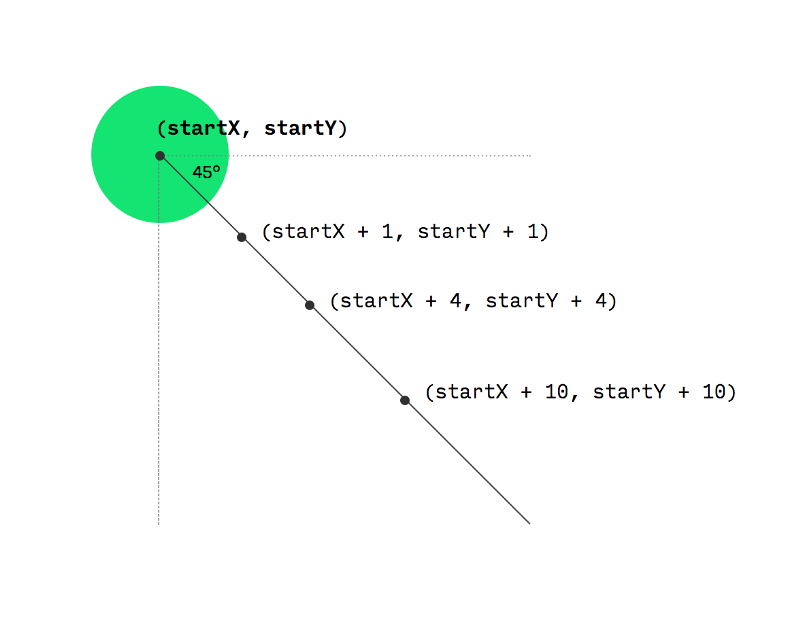
现在有很多方法可以使用三角函数和所有的math-e-matics算到任何你想增量的x和y的值。但是当你有线性插值,你为什么还要这么做呢?
如果你对线性插值没有任何的概念,建议你可以阅读《线性插值》这篇文章,先对线性插值有一定的了解,能帮助你更好的理解下面的内容。
线性插值方法
下面就是一个线性插值函数,常称为lerp,其看起来像这样:
function lerp(min, max, fraction) {
return (max - min ) * fraction + min;
}
可以通过一个滑块来帮助我们理解线性插值,其中min在滑块的最左端,max在滑块的最右端。

接下来是选择我们需要的fraction(fraction常称为缓动因子)。lerp可以选择一个fraction值和计算出min和max之间的一个值:
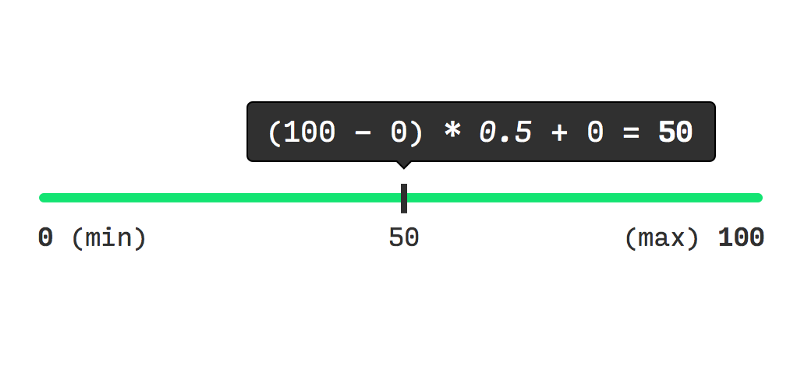
如果把lerp函数中的fraction设置为0.5,这样一来,介于0(min的值为0)和100(max的值是100)中间值就相当于50。
类似的,如果我们选择fraction的值为0.85:
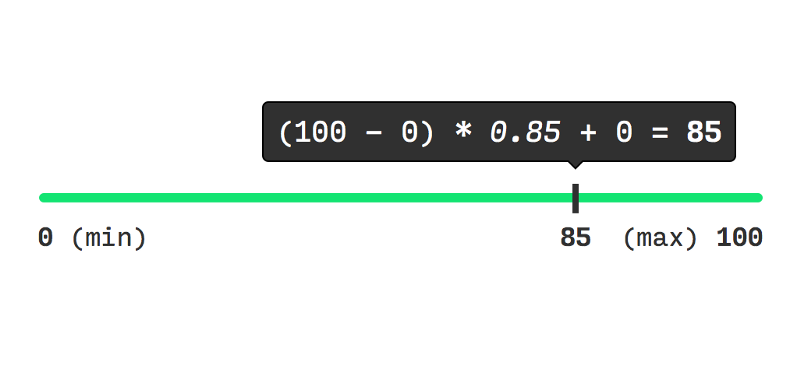
同样的,如果让fraction = 0时lerp计算出来的值为0(等于min值),如果让fraction = 1时lerp计算出来的值为100(等于max值)。
我选择0和100是min和max的值,只是帮助我们更好的理解lerp函数,事实上lerp可以选择任意的min和max值。

lerp允许你选择fraction的值介于0 ~ 1之间以及任何你想要的min和max值。当lerp中选择的fraction值为0时,计算出来的min和max的中间值是min;如果你选择的fraction的值为1时,计算出来的min和max的中间值是max。如果fraction选择0 ~ 1之间的任何值时,可以计算出min和max之间的值。关键是,你可以看到lerp中的min和max中让动画效果和传统动画之间有何不同之处。
好了,如果有人给出的lerp的fraction的值超出了0 ~ 1之间的范围呢?你也看到了,lerp公式是一个非常简单的数学运算。这里没有欺骗和不好的值,想象一下扩展滑块的两个方向,不管lerp的fraction值都希望产生一个合乎逻辑的结果。而我们在这里不应该把时间花费在讨论lerp不好的值,而应该花更多的时间考虑如何将lerp的特性运用到球体的动画中。
基于前面的update()函数。借助lerp函数对update()函数中的x和y值做相应的处理:
function update() {
context.clearRect(0, 0, width, height);
drawBall(x, y, 30);
x = lerp(x, endX, 0.1);
y = lerp(y, endY, 0.1);
requestAnimationFrame(update);
}
下面的示例是我们改良过的动画效果,试着在下面的示例中在不同的位置点击鼠标:
是不是很平滑?这就是lerp让动画发生了什么。
大家或许也注意到了,代码中x和y的变量最初的初始值为别为startX和startY——设置了球的在任何帧的当前位置。这里设置了fraction的值为0.1,事实上你可以选择任何你想要的fraction值,但需要记作的是,选择的fraction将会响影动画的速度。
在每一帧x和endX的fraction值是0.1,其中x相当于lerp的min,endX相当于lerp的max,这样通过fraction就可以计算出新的x值,同样y和endY相当于lerp中的min和max,fraction同样是0.1,这样可以获取新的y值。

在新计算出来的(x, y)坐标将绘制出新的球。
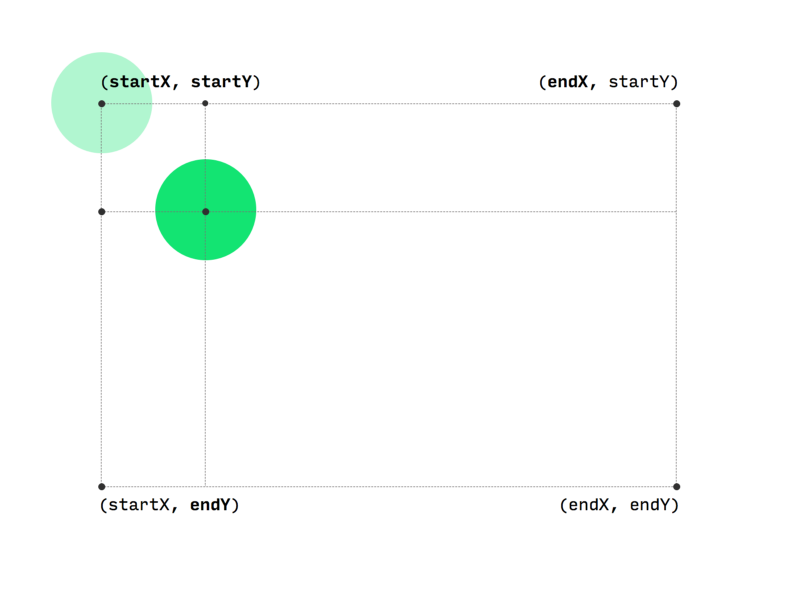
重复这些步骤,直到x变成endX和y变成endY,这种情况下min=max。当min和max变成相等时,lerp可以计算出相同的值(min/max),直到动画停止。
这就是球是如何运动的。在这篇文章中,我们开始定义关键帧和中间画的是什么。然后我们试着简单的方法画动画,同时加以思考。最后用线性插值达到我们能够实现的目的。
我希望所有的数学对你是有意义的。欢迎继续在更多的地方使用线性插值的概念。@Rachel Smith在Codepen上写了一篇有关于动画中线性插值的文章,而这篇文章的灵感就是来源于这篇文章。@Rachel Smith在文章中写了好几个例子,你一定要点开看看其效果。
如果你喜欢这篇文章,欢迎你将这篇文章分享给你的朋友。当然,如果你有更多关于线性插值相关的知识,欢迎在下面的评论中与我们一起分享。
本文根据@Nash Vail的《Understanding Linear Interpolation in UI Animation》所译,整个译文带有我们自己的理解与思想,如果译得不好或有不对之处还请同行朋友指点。如需转载此译文,需注明英文出处:https://medium.com/@nashvail/understanding-linear-interpolation-in-ui-animations-74701eb9957c。
如需转载,烦请注明出处:https://www.fedev.cn/canvas/understanding-linear-interpolation-in-ui-animations.htmlAir Jordan 3 For Kids-033

