【转载】运动曲线提升CSS动画效果
本文转载自:众成翻译 译者:鞠大宝 链接:http://www.zcfy.cc/article/1162 原文:https://www.smashingmagazine.com/2016/08/css-animations-motion-curves/
先有UI动画,然后才会有好的UI动画。好的动画会让人惊叹“哇哦!”——因为页面看上去很流畅、很漂亮,最重要的是,自然,一点都不会让人觉得不和谐或者僵硬死板。如果你经常逛Dribbble或者 UpLabs这类网站的话,你就会明白我在说什么了。
一些极好的拓展阅读资源:
既然有这么多天才设计师创造了如此漂亮的动画,自然是任何开发者都会想要在自己的项目中引进这些效果。如今,CSS为
transition-timing-function提供了一些预置变量,比如ease-in,ease-out和ease-in-out, 它们将页面的平滑感和真实感提升了一个档次,但是,你不觉得这个方法太大众化了吗?试想如果页面上的每个动画都用了这3个相同的时间变量,那该是有多乏味啊。 ——(引自: Lukáš Straňák)
transition-timing-function有一个变形是cubic-bezier(n1, n2, n3, n4), 你可以传进4个参数来创建自己独一无二的时间函数。在这篇文章的最后,你将会看到这4个参数各自代表什么——但是,相信我,要找到四个数字来捕获你想象中的转变并不是一件容易事儿。 幸亏有cubic-bezier和Ceasar, 你不必非得自己来完成。这些工具将运动曲线引入到了网页中。——(引自: m-2-h)
运动曲线最早是被动画师们用来创造先进、逼真的动画(比如 Adobe After Effects)。通过cubic-bezier 和Ceasar, 你可以很容易地操纵曲线的形状,另外 (n1, n2, n3, n4) 这4个数字也会为你填好,这绝对超赞! 尽管如此,如果使用时想要最大化运动曲线的功能,你则需要了解它们的工作原理,这就是我们接下来在这篇文章中要讲到的。现在我们开始吧。
理解运动曲线
运动曲线其实只是连接 动画属性 和时间的一个点。一条运动曲线展示了一个动画运动的速度是如何受时间的影响并随之变化的。
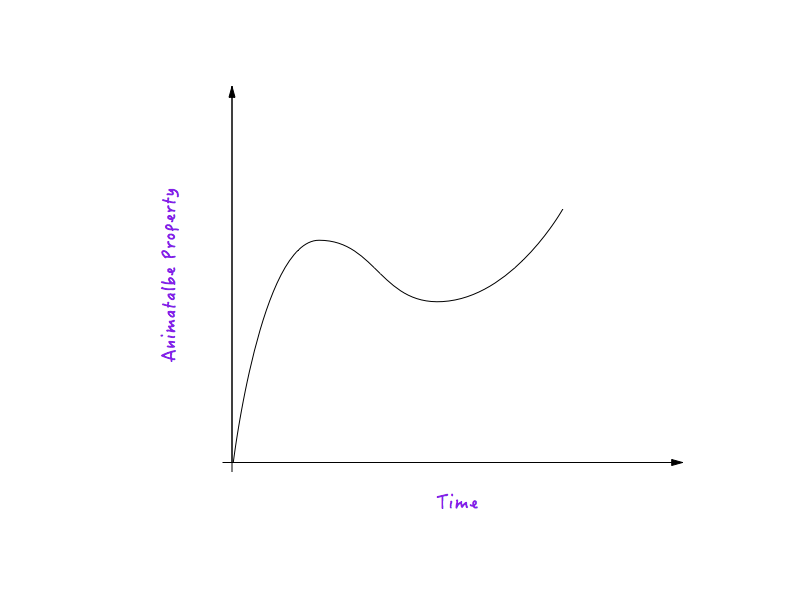
运动曲线是连接动画属性和时间的一个点。
让我们拿 distance (translateX) 作为动画属性举例。(这个解释同样适用于其他的任何一个动画属性。)
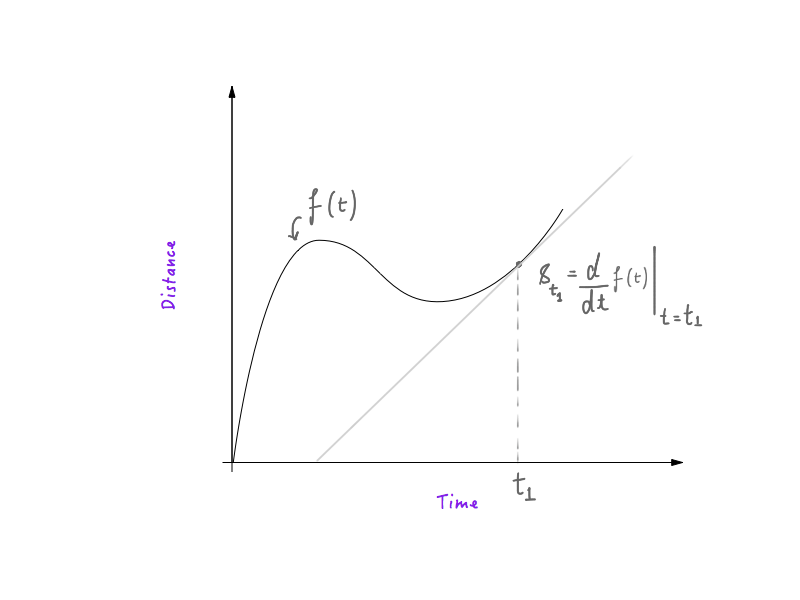
在一张距离 —— 时间图上计算t1时刻的速度。
如果你有一定的物理学和初级微积分学的基础,你就会知道从一张距离 —— 时间表上算出速度是非常容易的。表中的单位时间内走过的距离除以单位时间得到的某时刻的导数,就是速度。 也就是说,距离 —— 时间曲线上的物体在曲线陡峭的地方有更快的运动速度,而在曲线平缓的地方,速度则比较慢。如果你知道它的原理,那太棒了!说明你已经做好了充足的准备,可以跳过下面这节。
如今,我意识到设计和开发是完全不同的领域,毕竟不是每个人都有相同的背景。 也许上面那段话你完全听不懂,也用不着灰心丧气,因为我接下来会慢慢解释的。
看到下面的红盒了吗?请允许我童心未泯地将之称为“Boxy”;这样提及它时会更方便一些。好了,我们可以看到Boxy正在以线性的方式从屏幕的一边移动到另一边,接下来我们来分析一下它的运动。
transition-timing-function 的一个预置参数是linear。为了让Boxy动起来,我们要做的就是添加下面的这个方法。
.moveForward {
transform: translateX(1000px);
}
为了控制动画效果,我们会为Boxy设transition属性,如下所示:
#boxy {
width: 200px;
height: 200px;
background: red;
transition-property: transform;
transition-duration: 1s;
transition-timing-function: linear;
}
想要将transition解释清楚是一件很麻烦的事情,实际上,你将会发现transition都是用速记形式写的:
#boxy {
width: 200px;
height: 200px;
background: red;
transition: transform 1s linear;
}
看它动起来的效果。

红盒在做直线运动。
它看上去很像一个机器人,不是吗?当然你可以说它之所以看上去很机械,完全是因为它做的是直线运动,这听起来好像很合理。但是你又要如何解释导致这一现象的原因呢?我们可以看到直线运动使得物品的移动显得很机械,但是隐藏在屏幕后面的工作原理又是什么呢?所以,我们的当务之急就是搞清楚为什么这样的移动会让人觉得很机械、不和谐又不自然。
让我们将Boxy的移动用坐标轴来展现,看看是否能得到一些有用的信息。坐标轴有两根轴线,纵轴表示距离,横轴表示时间。Boxy在1s内走过了1000px的距离。 我们接下来会用到一些数学知识,不过不用担心,因为都很简单。
这就是我们建的非常简易的图表,上面有两根坐标轴, 正如我刚刚提到的那样。

只有坐标轴的空表。
现在,它是空的,让我们填进去一些数据。
首先,我们可以看到在初始时刻(也就是0s时),动画还没有开始,Boxy处在它的初始位置(也就是0像素的位置)。1s过后,Boxy一共运动了1000px,停在了初始位置的对面。

Boxy的起点和终点位置。
让我们在图中标出数据。
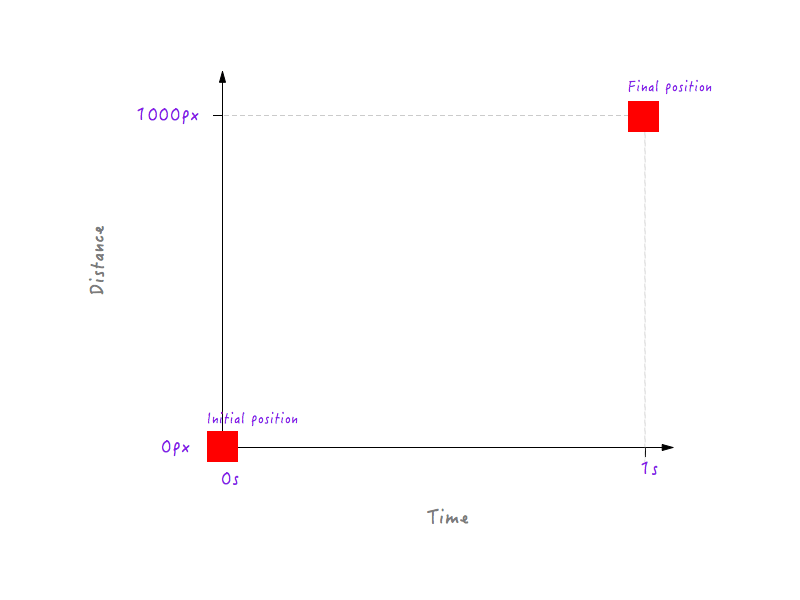
标有Boxy起点和终点位置的图表。
到现在为止一切都很顺利。但是只有两个点的数据远远不够——我们需要更多。接下来的数据记录了Boxy在不同时间点的所处位置(这一切都多亏了我的高速摄像机)。
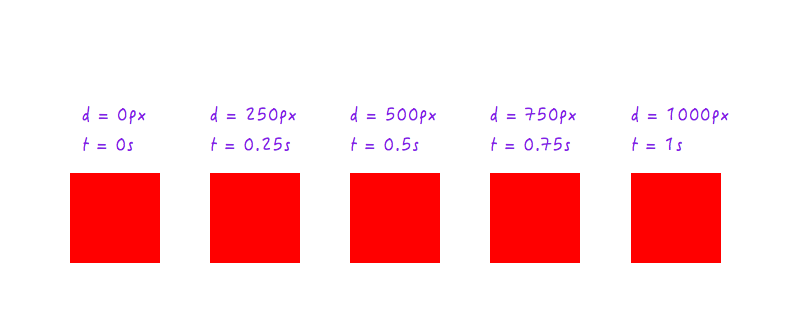
*不同时间点Boxy所处的位置 *。
我们将这些数据添加到坐标轴中。
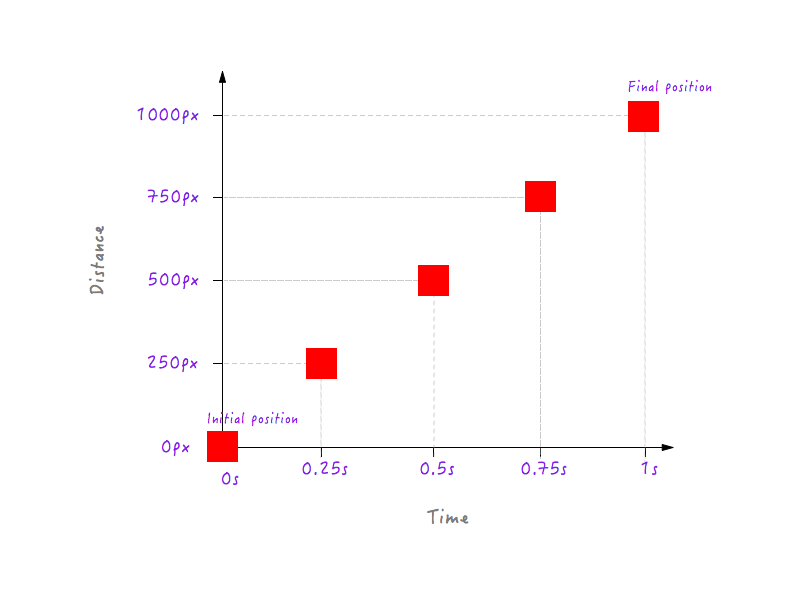
标有不同位置的坐标轴。
当然,你也可以搜集更多不同时刻的点(比如0.375s、0.6s等等),但是我们现在有的已经足够来建成这张表了。标注了上面的所有点后,我们的表就建成啦。来,击个掌!
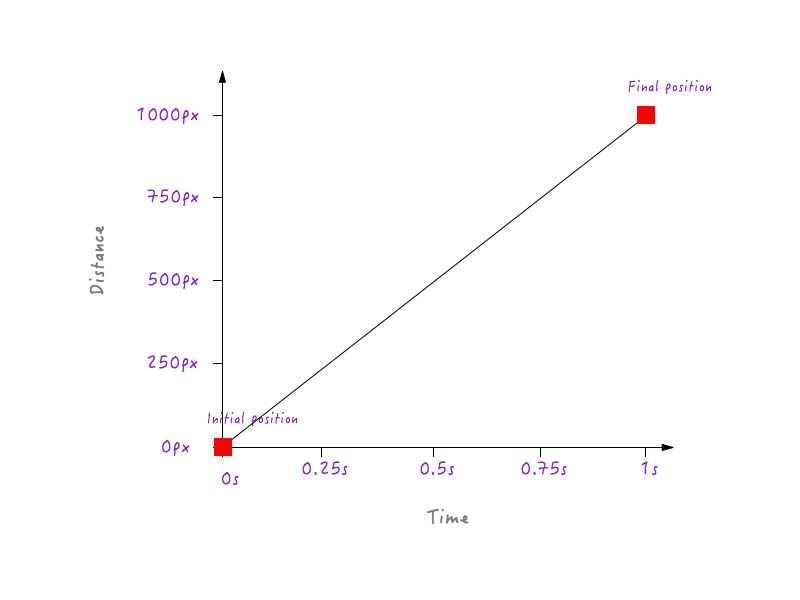
坐标轴最终版本。
酷!但是我们能从这得到什么呢?我们要时刻记住,实验的目的是弄明白为什么Boxy的线性运动看上去会不自然并且很机械。很显然,我们建好的这张表还不能告诉我们这是为什么。我们需要更深入地探索。
让我们记住这张表,然后花1分钟时间来讨论一下速度。我相信你应该了解速度的概念——我指的就是数学术语上的速度。它的计算方法如下所示:

计算速度的数学公式。
因此,如果一辆卡车在1小时内行驶100公里,我们就说它的速度是100km/h。

速度的计算。
如果这辆卡车将速度加倍,他就会在相同的时间间隔1小时内行驶双倍的距离(也就是200公里),换句话说,要行驶100公里,它现在只需要刚才的一半时间(也就是半个小时)。能理解我的意思吗?
类似的,如果这辆卡车将它的速度减半,它将在相同的时间段1小时内走过50公里,也就是说,要行驶100公里,它将需要双倍时间(也就是2个小时)。
好!让我们回到之前的思路上,我们目前是在尝试弄清楚这张距离-时间表是如何帮助我们找到Boxy的线性运动看上去很僵硬的原因。
嘿,等一下!我们有一张距离-时间表,并且速度可以通过路程和时间求得,不是吗?接下来我们就尝试计算Boxy不同单位时间内的速度。
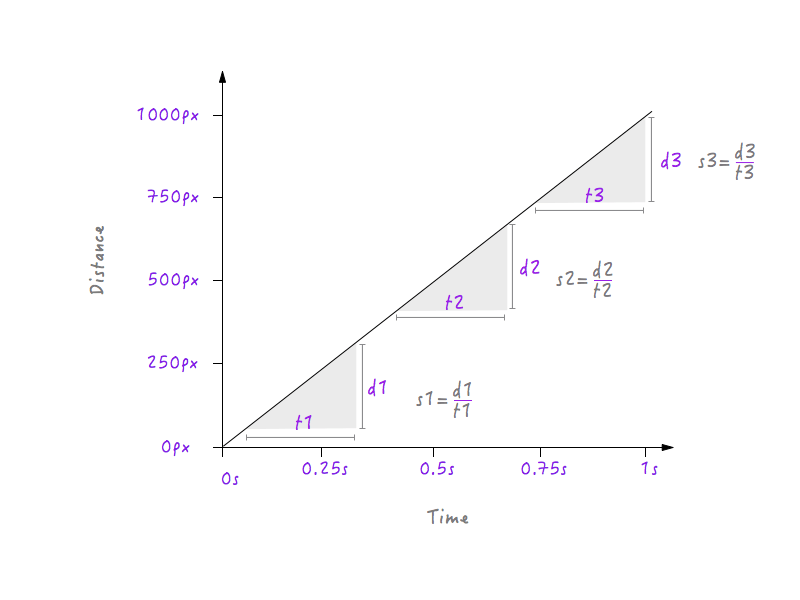
计算不同单位时间段的速度。
在这里,我挑选了3个不同的时间段:一段靠近起点,一段在中间位置,还有一段是接近终点的位置。很明显,在这三个时间段内,Boxy速度相同(它运动的路程s1=s2=s3),即1000px/s。由此可见,不管你在上表中选择的是哪个时间段,你会发现Boxy都是以1000px/s的速度移动的。是不是很意外?现实生活中,没有物体能够一直以一个恒定的速度运动;它们起步时速度都比较慢,然后会逐渐增加速度,运动一段时间后,又会在停下来之前减速,但Boxy却是以1000px/s的速度突然起步,接着做匀速运动,并且恰恰是以相同的速度突然停止。这就是为什么Boxy的移动看上去很机械且不自然,接着我们必须重新绘制我们的坐标系来体现这一点。但是在深入研究之前,我们需要了解速度的改变是如何改变距离-时间表的。准备好了吗?接下来的探索将会很有趣。
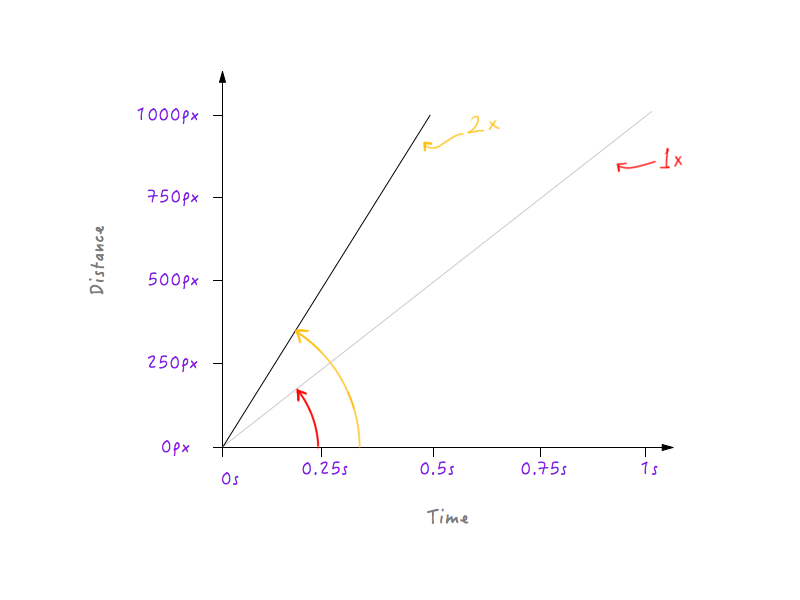
我们将Boxy的速度提升一倍,来看看坐标图相应地会如何变化。Boxy的初始速度,还是如我们上面计算的那样是1000px/s。因为我们将它的速度变为了两倍,Boxy只需一半时间——也就是0.5s,就可以走完全程。让我们在坐标图中画出来。
两倍速度时的坐标图。
如果我们将它的速度增加至3倍呢?Boxy只需要三分之一的时间就可以走完全程(也就是1/3s)。
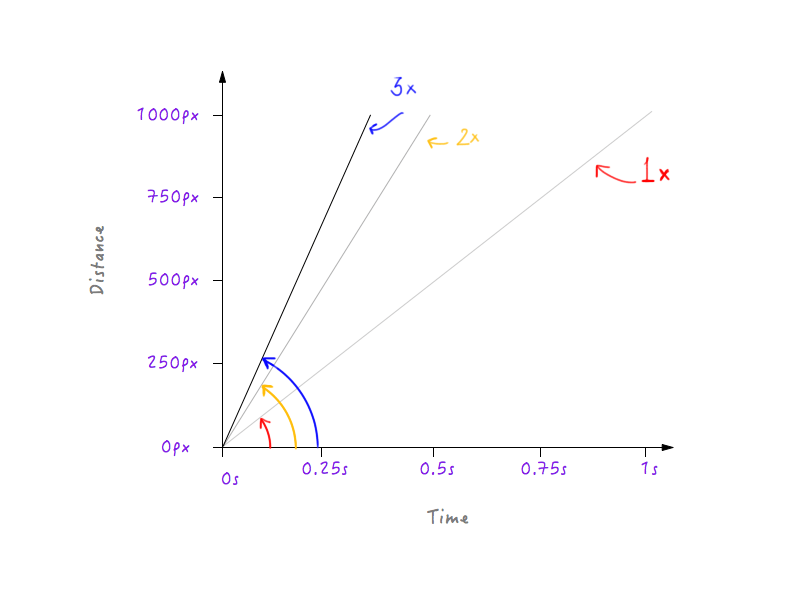
三倍速度时的坐标图。
嗯,看出什么了吗?我们可以看到,随着速度的增长,坐标图发生变化,这条直线与时间横轴间的夹角也在不断增加。
那好,我们继续将Boxy的速度减半。将它的速度减半意味着Boxy只能在1秒钟内走过500px(也就是刚刚距离的一半)。然后让我们在坐标图中画出来。
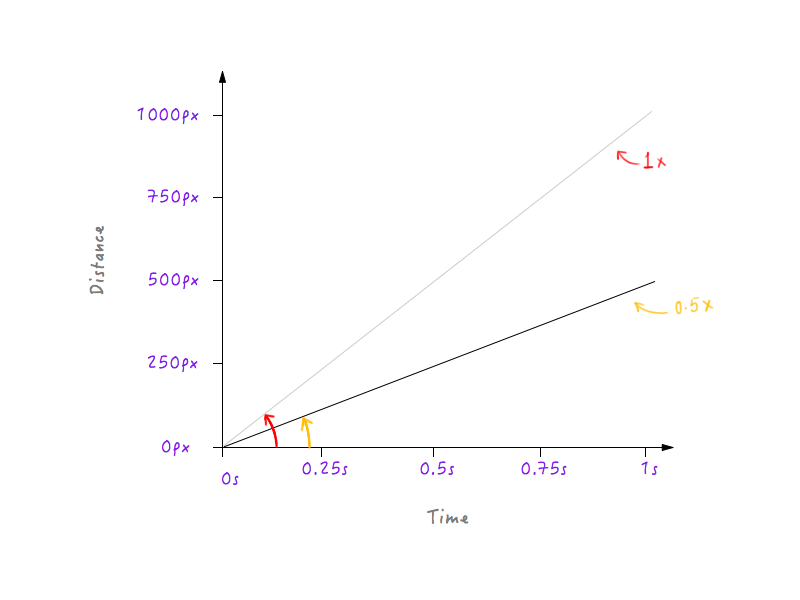
一半速度时的坐标图。
我们将Boxy的速度再放慢一些,让它以原本速度的三分之一运动。这样的话,1s内Boxy就只能走过一开始走过路程的三分之一。
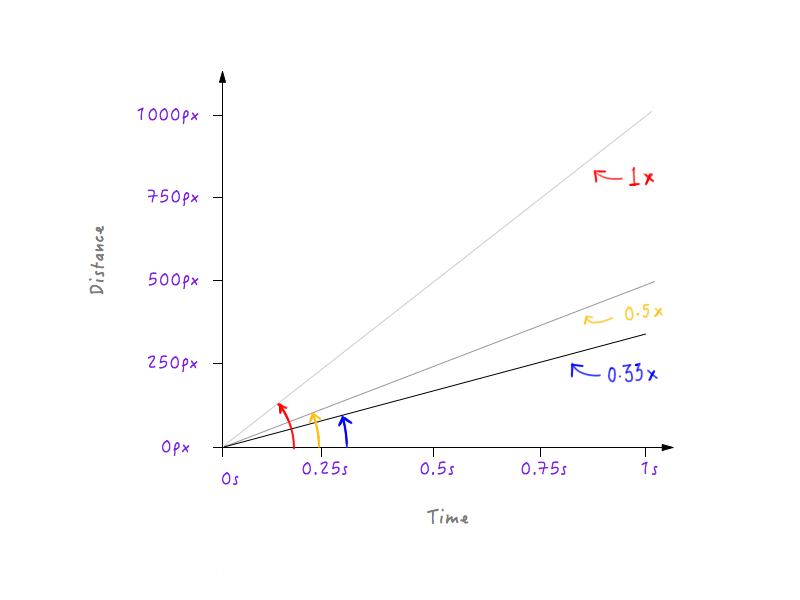
三分之一速度时的坐标图。
看出规律了吗?我们增加Boxy的速度时,线条越来越陡峭;而减慢Boxy的速度时,线条又变得平滑。
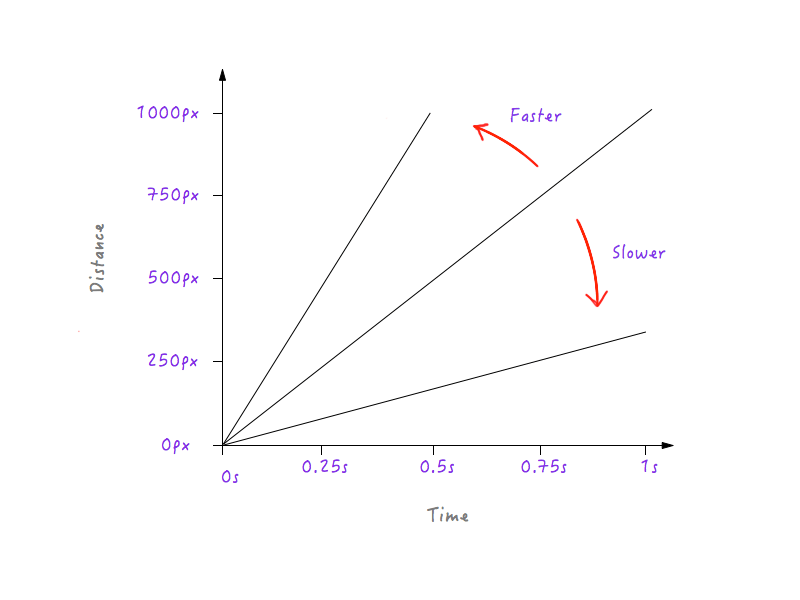
速度增加时直线变陡,减慢时直线变得平缓。
这个结论很重要,因为对一条很陡的直线而言,也就是速度更快时,一小段时间内Boxy走过的路程会变化很多。
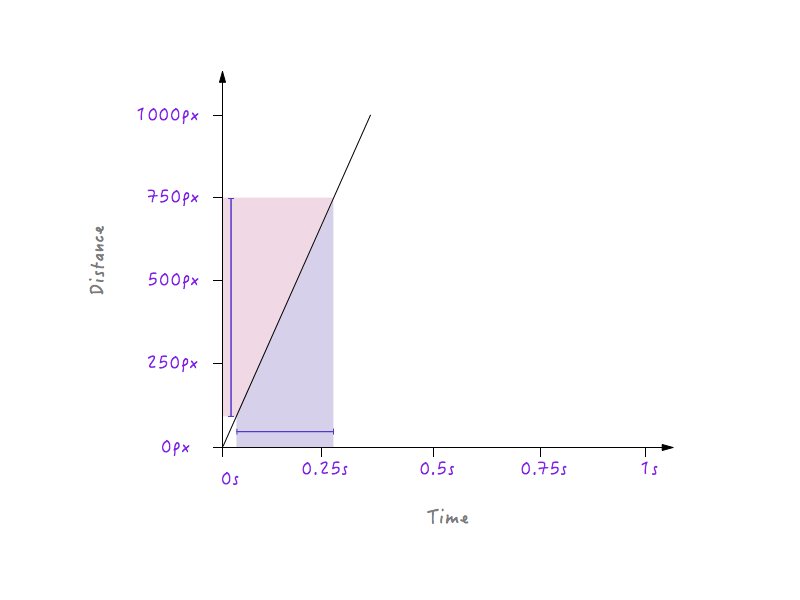
对线段更陡的表而言,小段时间相应会在距离上有很大的改变。
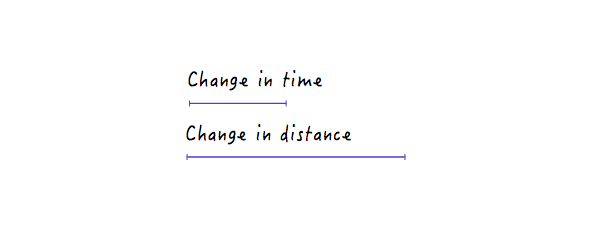
对线段更陡的表而言,小段时间相应会在距离上有很大的改变。
另一方面,对于坡度不那么大的直线,就算过去很长时间,距离上也只会变化一点点,这是运动速度比较慢的情况。
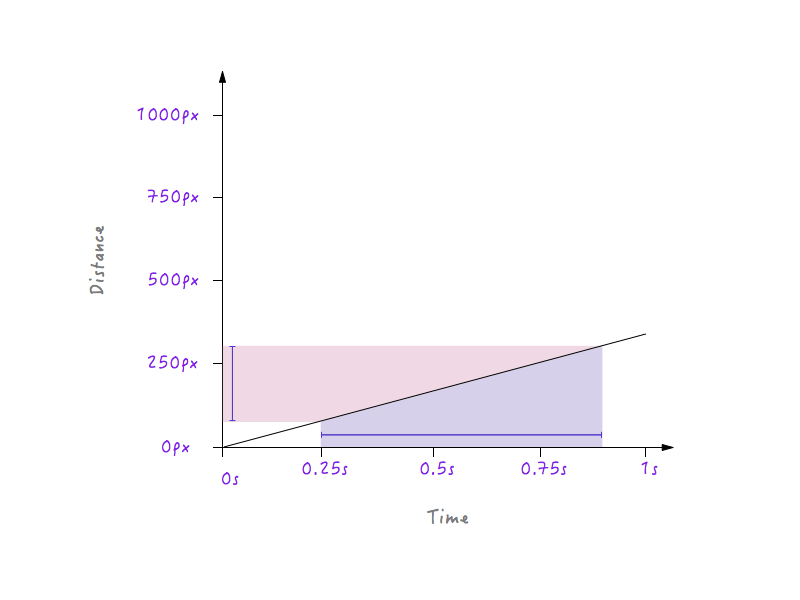
坡度比较平缓时坐标图中时间和距离的变化关系。
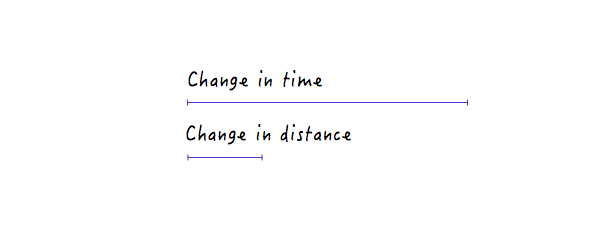
坡度比较平缓时,坐标图中时间和距离的变化关系。
以上我们所做的只是改变了Boxy的运动速度,它仍然是在做直线运动。但是,我们以新的方式弄清楚了距离和时间是如何改变速度的,接下来就可以绘制一张表来让Boxy以一种自然、真实的方式运动。
让我们一步一个脚印。首先,现实生活中的物体都是慢慢开始运动,并且逐渐增加运动速度的。所以,我们来模拟这一过程。
仔细观察下图,你会发现起点和终点位置没有变。因为我们不想改变动画的持续时间,也不想改变Boxy的运动距离。
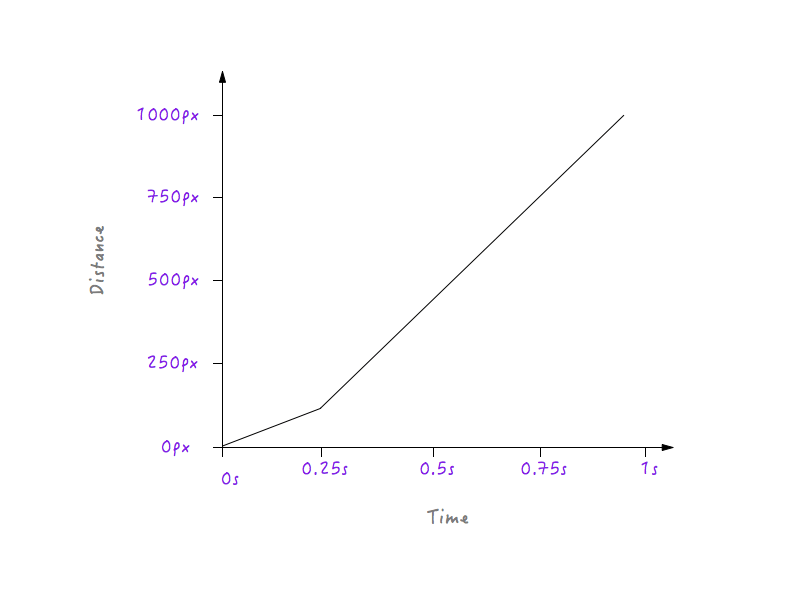
私人定制的运动曲线。
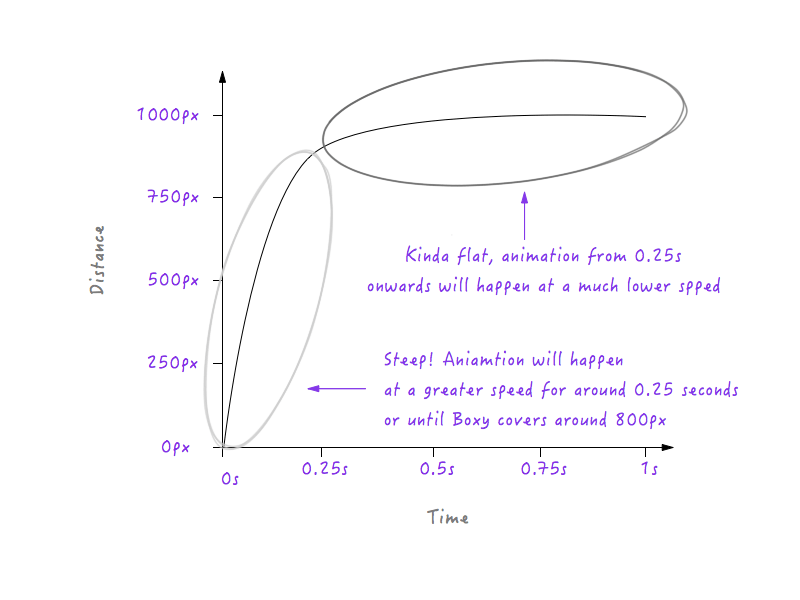
Boxy如果照着上面的这张图运动,前0.25s它的速度会比较慢,因为0s到0.25s之间这条线比较平缓,接着它会突然增速(因为0.25s之后线段突然变陡)。 但是我们需要将这一转变变得平滑,因为我们不想要任何转角——毕竟,这是一条运动曲线。接下来就将这个急转弯换成一条曲线。
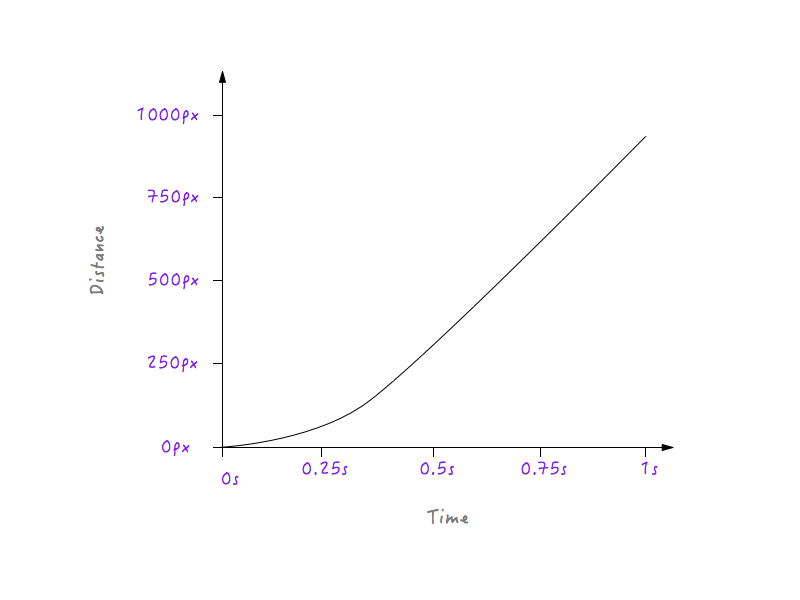
私人定制的运动曲线。
留心Boxy从静止状态到逐渐增速过程中平滑的转变。

按照上面那条运动曲线运动的Boxy。
很好!实际生活中,运动的物体停下来之前速度也是逐渐减慢的。让我们修改坐标图来适应这一变化。类似的,我们会在想要Boxy慢下来的地方增加一个点。就加在0.6秒处怎么样?我已经将这个转折点换成曲线了。
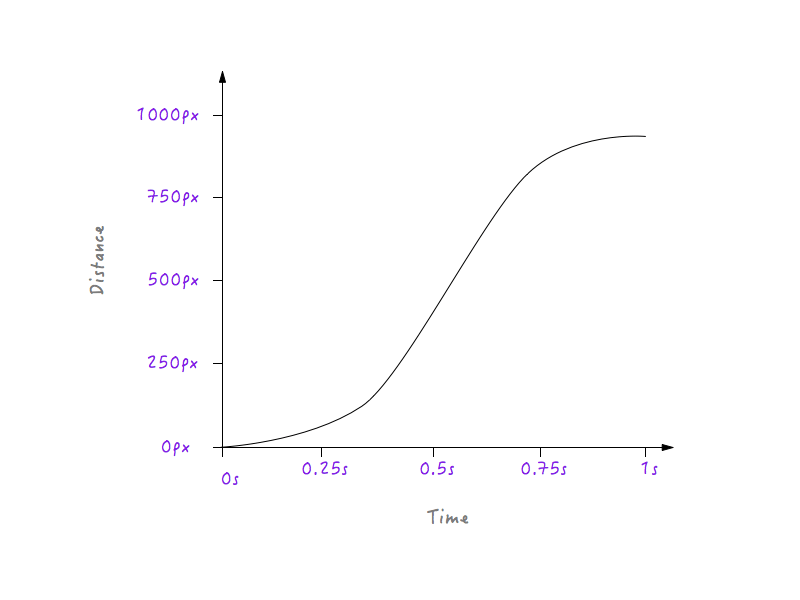
运动曲线终极版。
看Boxy动起来! 现在看上去自然了很多,不是吗?

按照终极版运动曲线运动的Boxy。
我们用来代替转角的曲线实际上是由很多短线段组成的;并且正如你已经知道的,表中的线段越陡峭,Boxy的运动速度就越快,线段越平缓,Boxy的速度就越慢。看坐标图的左边部分,会发现组成曲线的小线段坡度越来越大,导致速度逐渐增加;相应地,右边部分的线段越来越平缓,所以速度才会越来越慢。
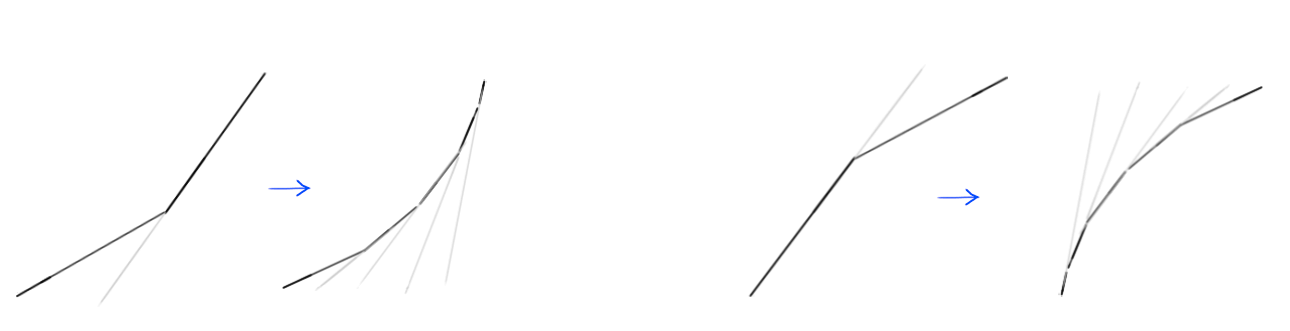
一条曲线只是很多的短线段的集合。
就以上我们所知道的,想要弄清楚运动曲线容易了很多。接下来我们来看一些例子。

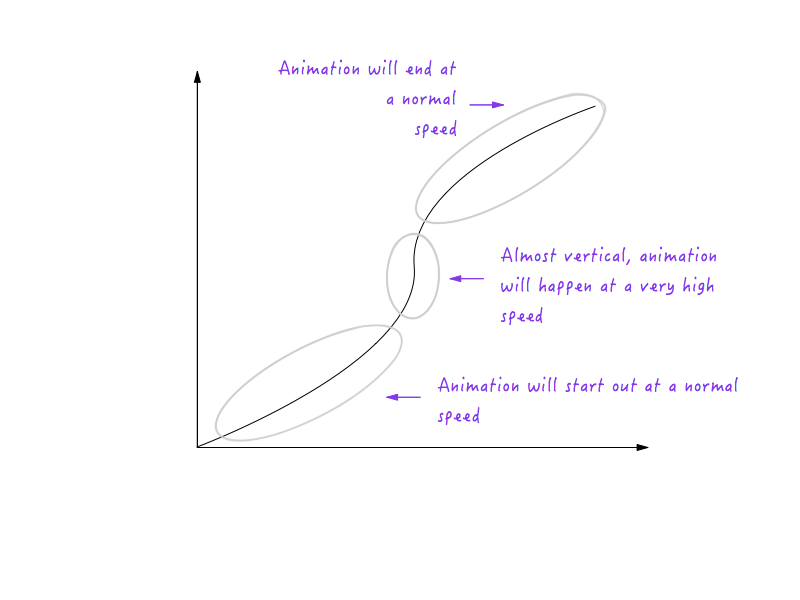

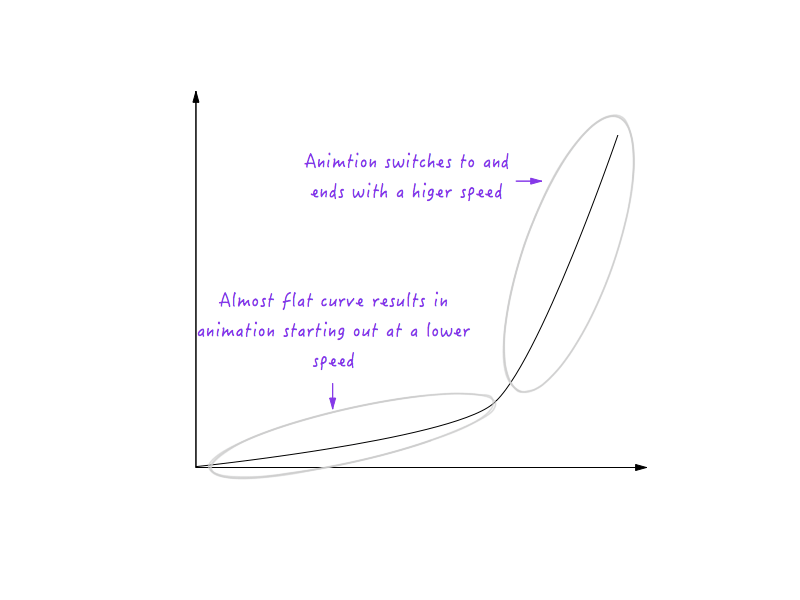

在UI动画中使用运动曲线
接下来你需要让一个UI元素动起来,可以将运动曲线为你所用。无论是一个滑杆儿、一个窗口模型,还是一个下拉菜单,增加适量的动画效果让它们看上去平滑自然可以大幅度提高你的用户界面质量。它会让用户对你的界面感觉良好。拿下面的滑出式菜单举个例子:
这是 Nash Vail (@nashvail)在CodePen上创建的Pen nJial。
点击菜单栏会从左边跳出菜单,但是这个出现的动作显得很生硬。CSS表的第51行将这个动画的transition-timing-function 设置为linear。这个动画效果显然可以优化。让我们使用cubic-bezier 来创建一个私人定制的定时功能。
如果你读到了这里,我猜你一定是个设计师或者开发人员,又或者两者兼是,因此,你对三次贝塞尔曲线一定不会感到陌生,很有可能至少遇到过1次。贝塞尔曲线的创造就是一个奇迹。 它们一开始是被用于计算机图形学来绘制形状,并且被用在Sketch和Adobe Illustrator这类工具中来绘制矢量图形。三次Bezier曲线使用如此广泛的原因是它们用起来非常方便:我们只需要改变4个不同点的位置,然后创造我们需要的曲线。
我们一般都会知道动画中物体的起点和终点位置,所以可以轻易锁定这两个点。然后就只要找到我们需要改变速度的两点位置。前两个固定的点被称为锚点,剩下的两个又叫控制点。
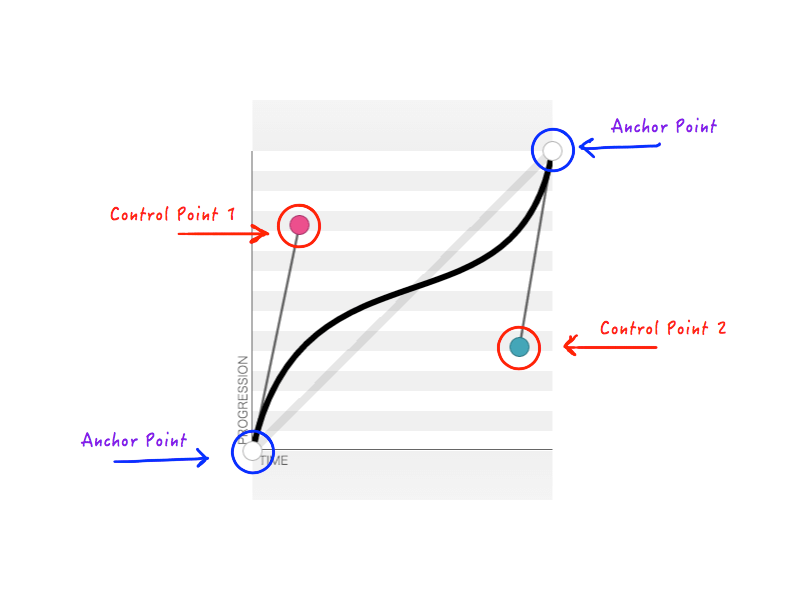
截取的贝塞尔曲线的一部分。
正如你所知,cubic-bezier 需要四个参数(n1, n2, n3, n4)来定制 transition-timing-function。这四个参数代表的是两个控制点的位置: n1, n2表示第一个控制点的x、y坐标点,n3, n4则表示第二个控制点的x、y坐标点。改变控制点的位置会使曲线的形状发生变化,n1, n2, n3, n4 全部或部分改变时我们的动画效果也会不一样。 举个例子,下面是传入参数为cubic-bezier(.14, .78, .89, .35)时的结果:
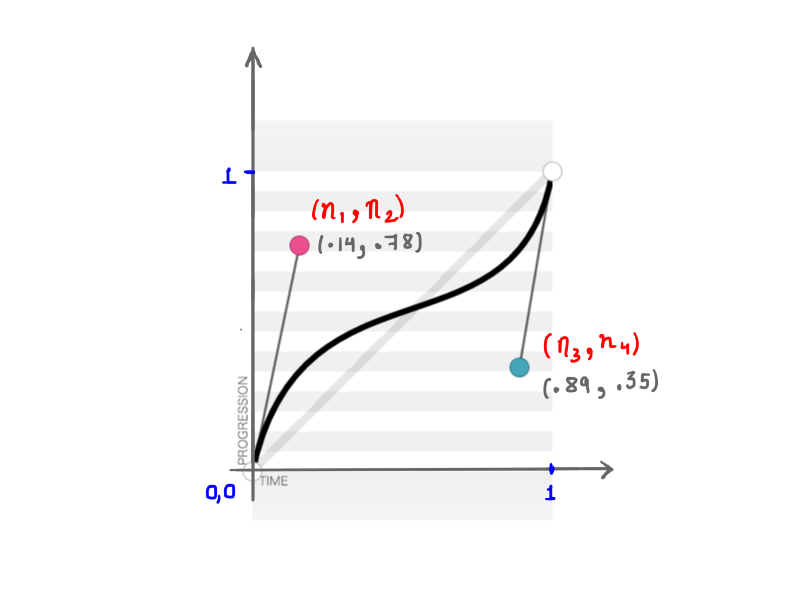
传入参数为(.14, .78, .89, .35) 的三次方贝塞尔曲线。
这些隐藏在看似简单的曲线背后的数学知识着实令人着迷。
好了,好了,让我们回想一下初衷:我们想借助三次方贝塞尔曲线来定制过渡时间功能的函数。我们需要的是能够快速滑出,然后速度逐渐慢下来,最后停止的菜单:
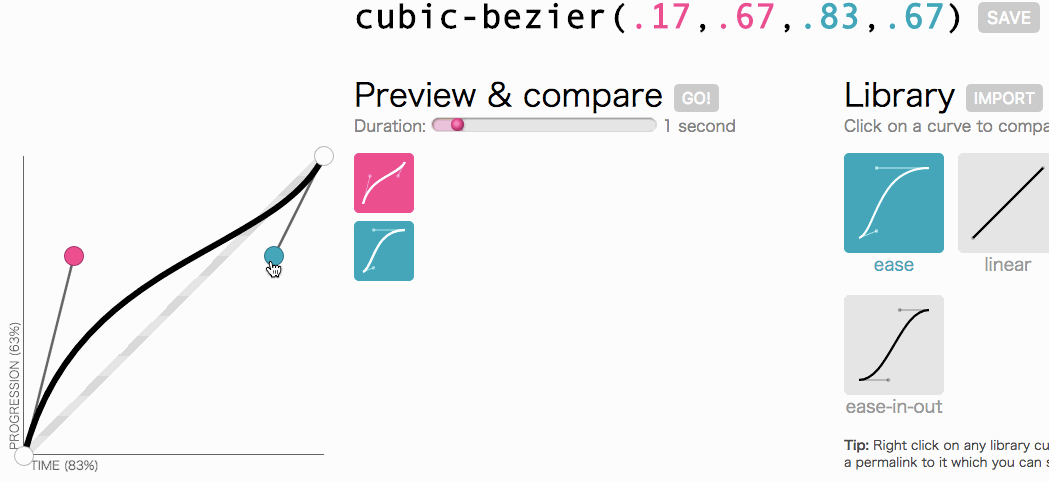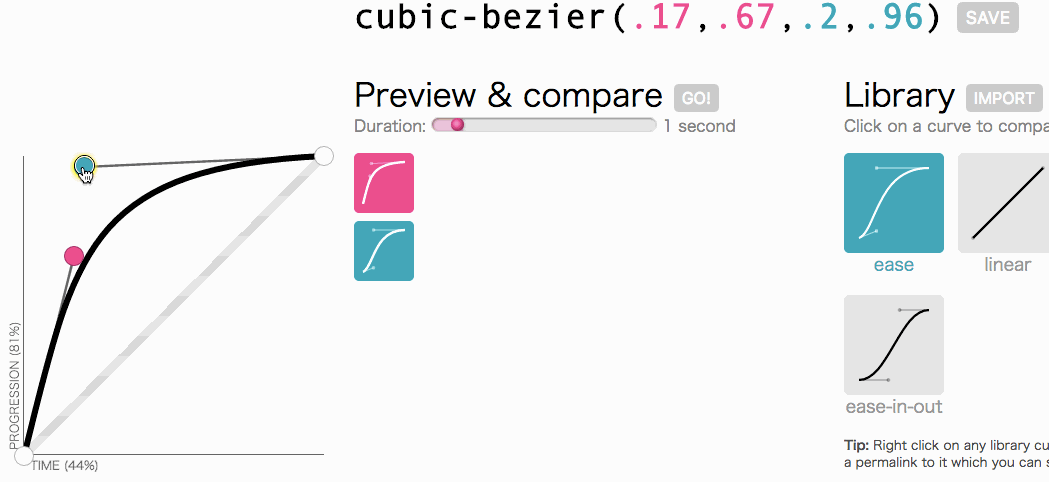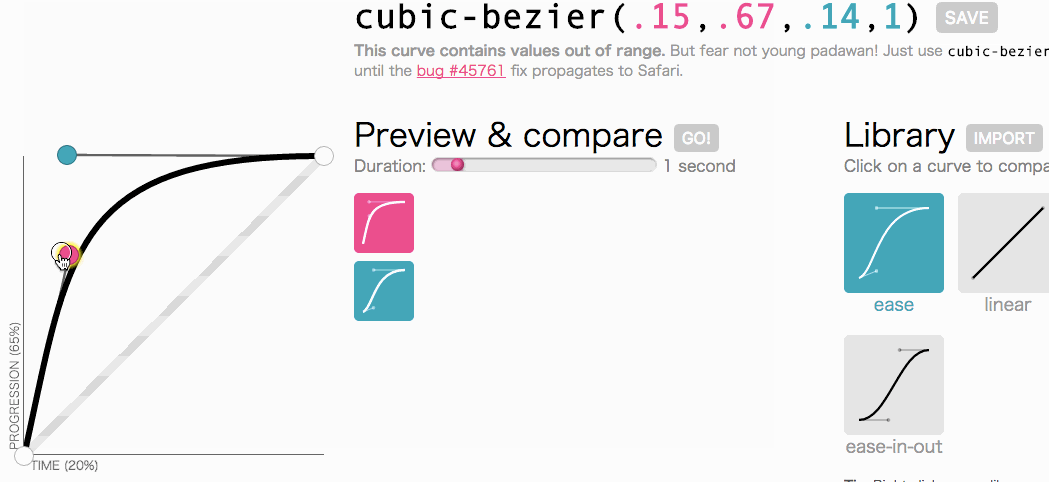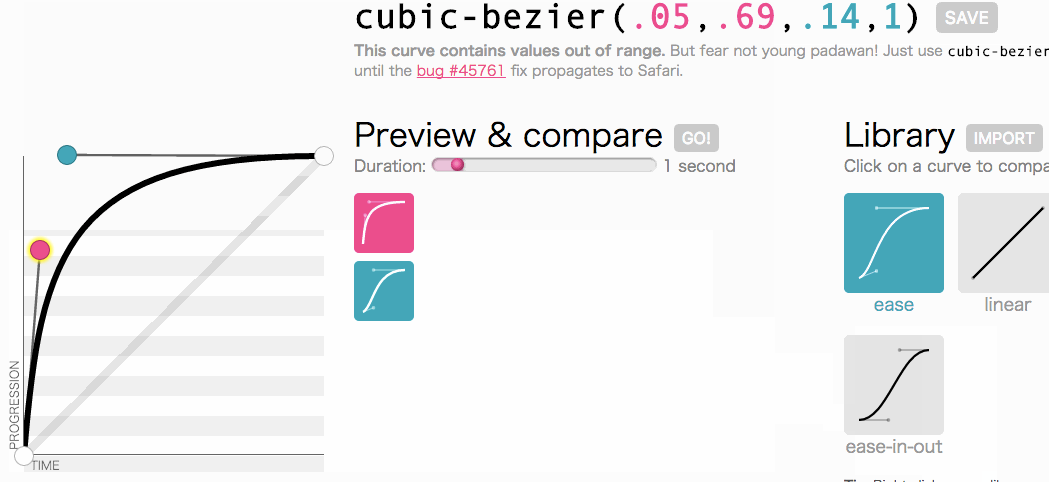
调整后的三次贝塞尔曲线。
看上去很不错。这个动画会开始很快然后逐渐慢下来,而不是全程都以一个恒定的速度移动。我只是简单地从上文中复制cubic-bezier(.05, .69, .14, 1) 然后拿它替换了linear。
这是Nash Vail (@nashvail)在CodePen发布的Pen nJial。
看到差别了吧?第二个版本看上去自然了很多,显得更有吸引力。试想,如果你的页面中每个动画都有一个自然定时功能,那将是有多赞啊?
由此可见,运动曲线一点都不复杂,它们理解、使用起来都非常简单。借助它们,你可以将你的UI页面提升一个档次。
我希望你已经明白了运动曲线的工作原理。如果你在使用运动曲线的过程中遇到了一些问题,或者你还根本没有用过它们,目前对你而言,让它们照你的意愿创造漂亮的动画,应该都是很简单的。毕竟,动画效果至关重要。jordans for sale blue
