三角函数在前端动画中的应用
特别声明,本文转载@Helkyle的《三角函数在前端动画中的应用》一文。
我是个很懒的人,开发过程中经常有意无意地刻意避开数学相关的知识,你也知道解数学题非常枯燥无趣。平时写动画也尽量使用 CSS3 来实现,timing-function 随意选用,最多也就调一下 cubic-bezier,找到看着舒服的就行。但是怎样让动画更顺滑,写出更贴近自然的动画,说实话以前我没怎么考虑过。
每次当动效设计师提出,能不能这样那样的时候,我会理所当然地予以否决。所以有很长一段时间,我非常羡慕那些能用 canvas 绘制很酷炫的动画的程序员。
先这样吧,又不是不会动。
今天来分享一下三角函数相关的内容,如果刚学前端的时候有人教我这些,我会很开心。
三角函数
三角函数已经是老生常谈了(街舞圈称之为 Old School),它伴随我们从初中到大学,太多的公式定理,光是应付考试就花了不少时间。先简单回顾一下,确保你还记得基础知识。
勾股定理
最开始学三角函数的时候就是从背勾三股四弦五开始,勾股定理描述的是对于直角三角形,直角两条边的平方和等于斜边的平方:
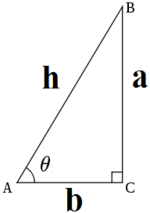
常用三角函数
印象中教科书里面只保留了 sin, cos, tan,其他可以通过变换得到。
sinθ = a / h
cosθ = b / h
tanθ = a / b
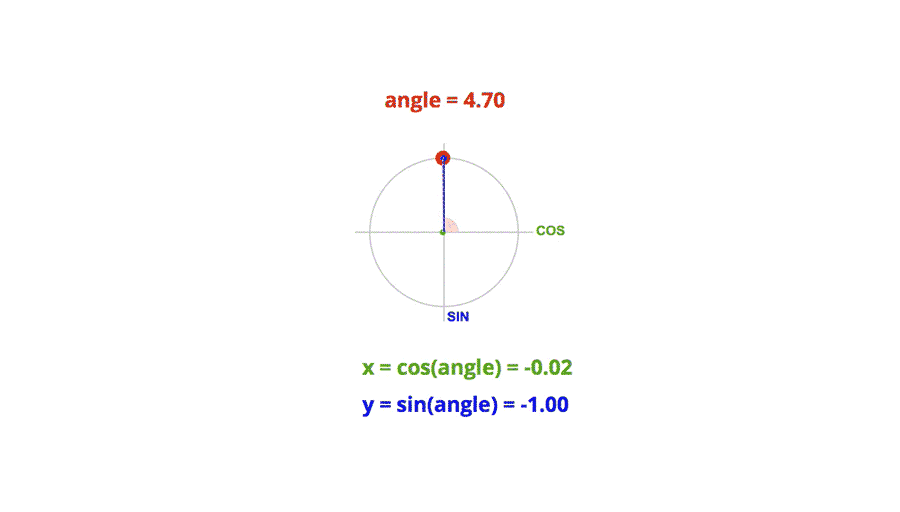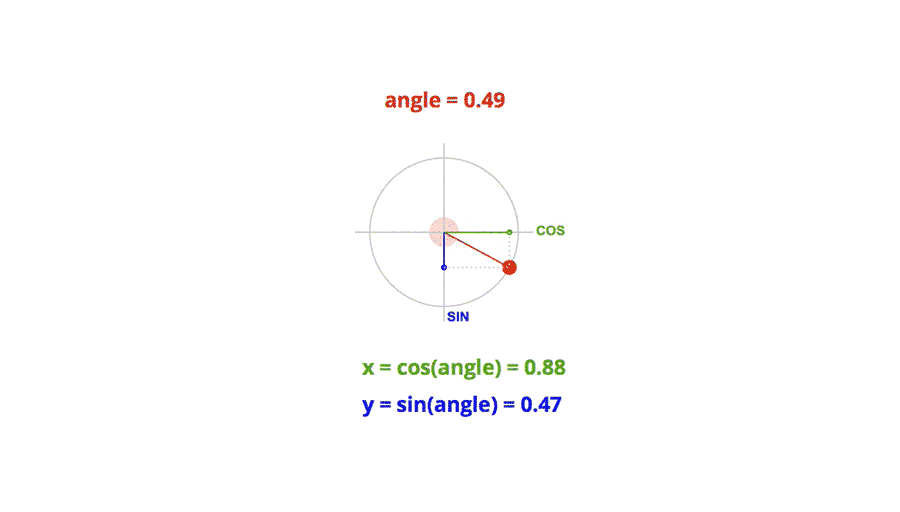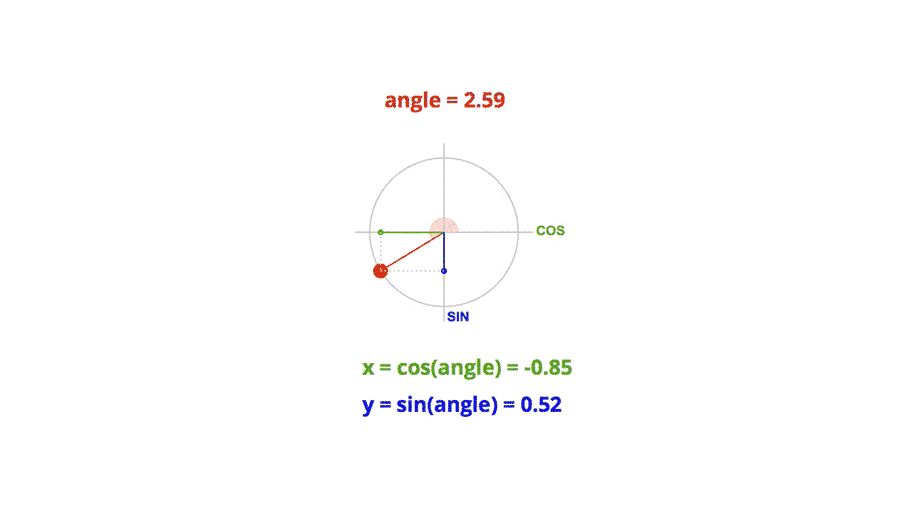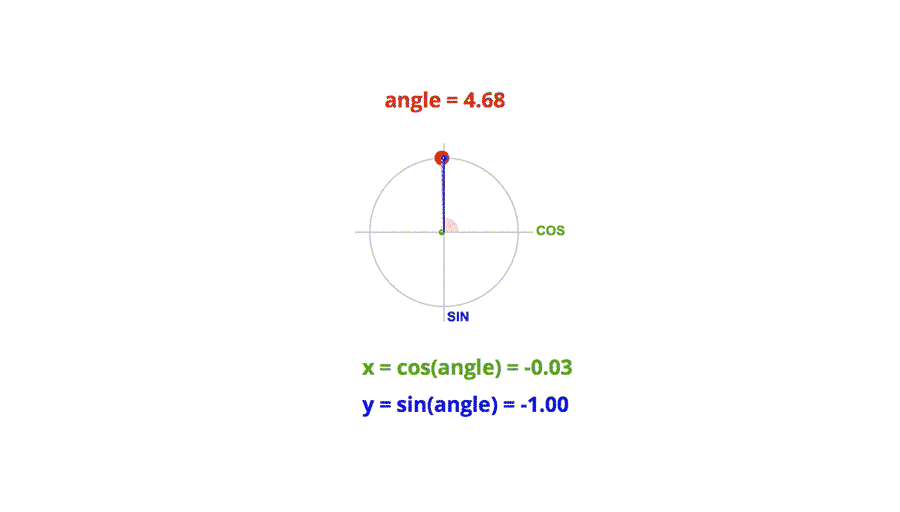
极坐标系和单位圆
在笛卡尔直角坐标系中,任一点 (x, y) 都可以转化成极坐标表示 (r, θ),其中:
r = Math.sqrt(x^2 + y^2)
θ = Math.atan2(y, x)
单位圆的定义是半径为单位长度的圆,圆上任意一点的横坐标就是对应角度的余弦值,任意点的纵坐标就是对应角度的正弦值。
简单的图像变换
以正弦曲线为例,对函数进行简单的变换,得到不一样的结果。

正弦曲线公式:y = A sin(Bx + C) + D
A控制振幅,A值越大,波峰和波谷越大,A值越小,波峰和波谷越小;B值会影响周期,B值越大,那么周期越短,B值越小,周期越长。C值会影响图像左右移动,C值为正数,图像右移,C值为负数,图像左移。D值控制上下移动。
这个公式非常有用,如果下文的代码让你不解,记得回来查看注解。
简单得回顾一下之后,确保你还记得这些基础知识,那么这些曾经被得滚瓜烂熟的内容,和前端代码结合会变成什么样?
常见的应用场景
图像应用
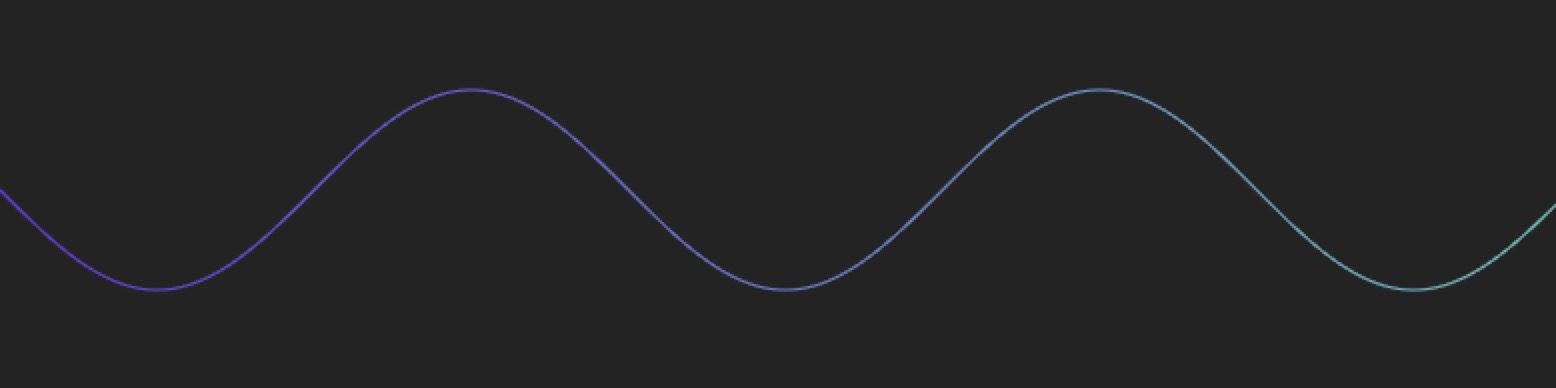
最直观的应用是使用三角函数来绘制 Wave 曲线
for (let x = 0; x < width; x++) {
const y = Math.sin(x * a) * amplitude
}
for (let x = 0; x < width; x++) {
const radians = x / width * Math.PI * 2
const scale = (Math.sin(radians - Math.PI * 0.5) + 1) * 0.5
const y = Math.sin(x * 0.02 + xSpeed) * amplitude * scale
}
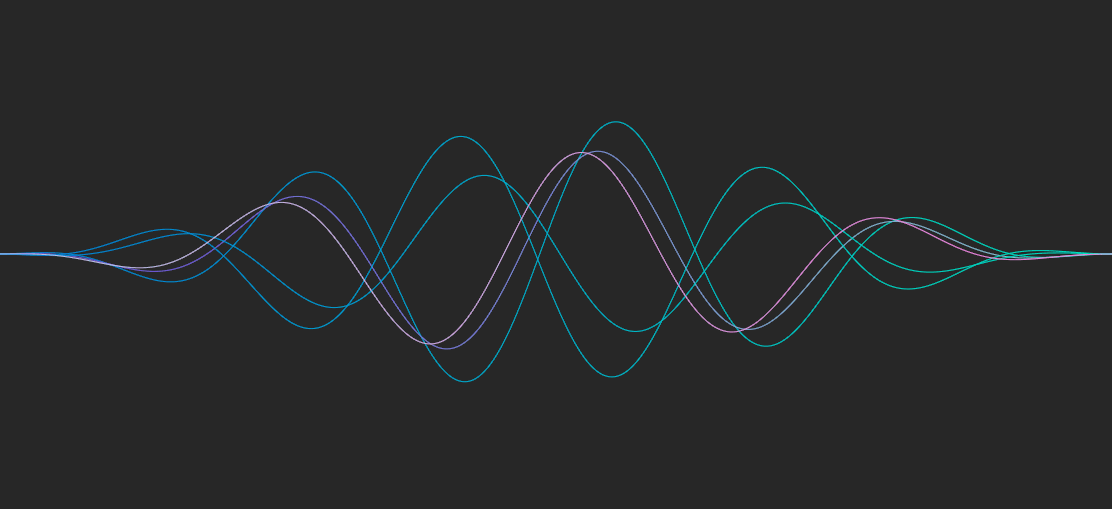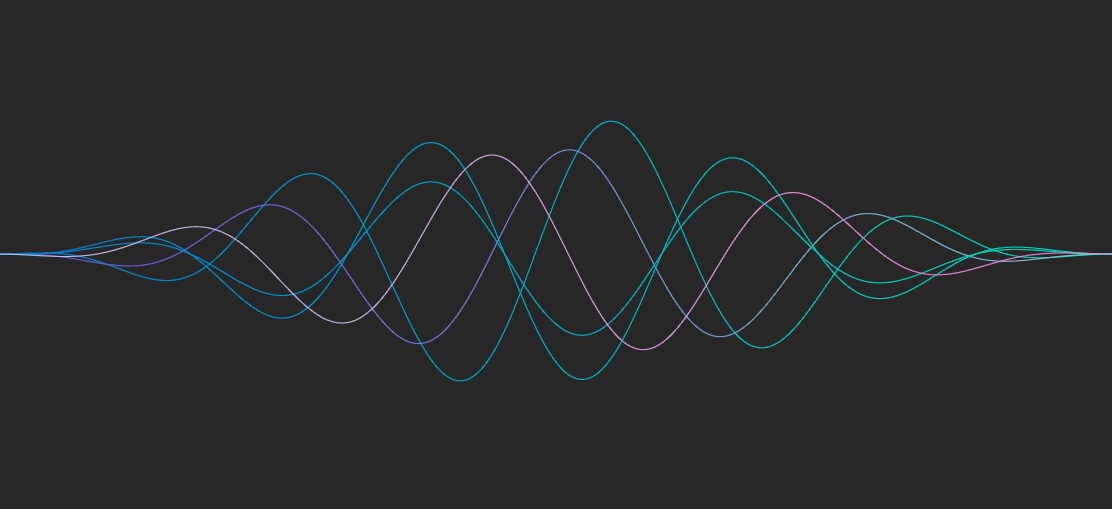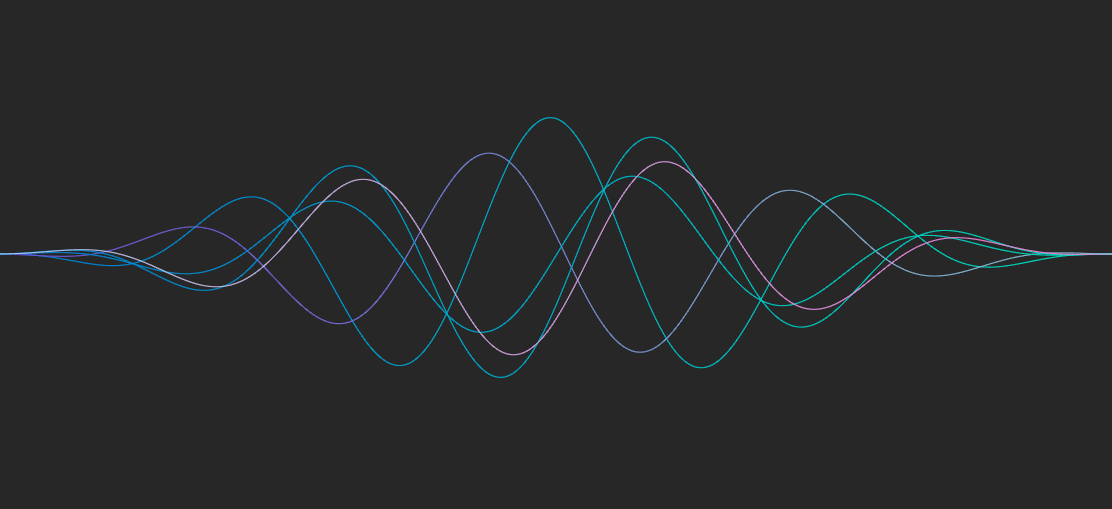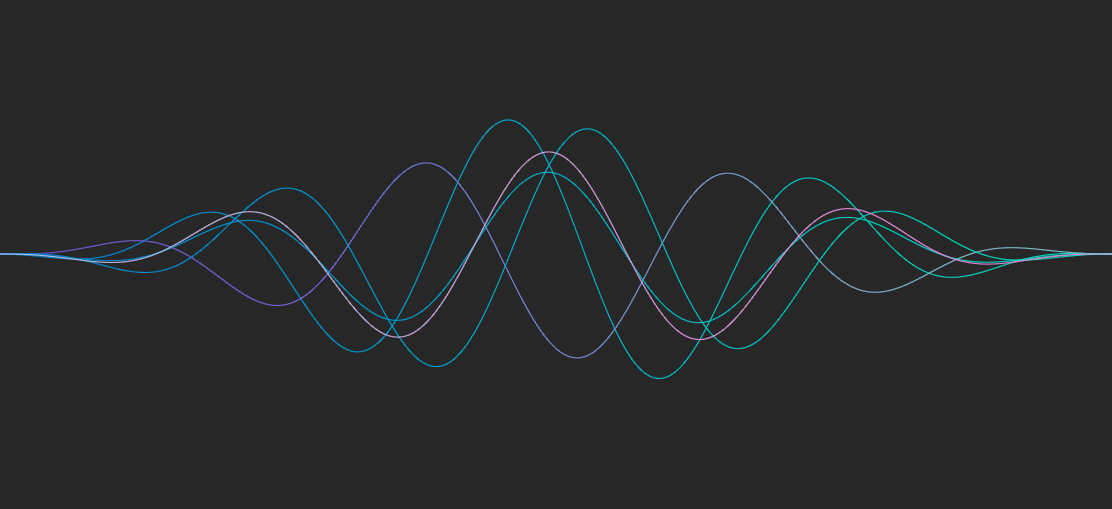
之前掘金上很火的一篇文章,也是同样的道理,使用两层正弦函数绘制曲线,fill 之后加上 stagger 动画,就能得到非常酷炫的水波效果。

如果再结合鼠标位置 + lerp 动画,就能实现坚果首页同款的动画。
这篇文章大部分代码都可以在我的 Codepen 主页看到。
SlowInSlowOut
正余弦曲线有很自然地缓入缓出的特性,并且在一个周期里面从 -1 到 1 再回到 -1,非常适合用来模拟一些物理效果。因为真实世界里面,汽车都是缓慢启动,加速,减速,再缓慢减速直到速度变为 0 的,突变会让人很难受。左边的摆球是线性匀速摆动,右边是用了三角函数优化的结果。显然左边的效果设计师会打人。

只需使用 sin 或 cos 乘以最大角度,就可以得到在摆动最大角度之间的 SlowInSlowOut。
ctx.rotate(Math.cos(t / 180 * Math.PI) * Math.PI * 0.25)
角度控制
在开发过程中,我们常常需要跟角度打交道,比如在头像左上角(45deg)显示 Notification 红点,用鼠标控制 rotation 等等。
前端 JS 里面 Math.atan2(y, x) 可以用来计算 (x, y) 和 x 轴正方向的夹角弧度值。
function getCurrentDegree () {
const deltaX = mouse.x - window.innerWidth * 0.5
const deltaY = mouse.y - window.innerHeight * 0.5
return Math.atan2(deltaY, deltaX) * 180 / Math.PI
}

插一句,三角函数相关的动画并不一定需要用 JS 来写,比如下面的 DEMO,使用 compass 依赖,同样可以做到灵活控制在特定角度的动画(千万不要手写各个点的坐标!!!后期没办法维护)
@import "compass";
.checkbox:checked {
~ button {
$per: 180 / 4;
@for $i from 1 through 6 {
&:nth-of-type(#{$i}) {
$angle: $per * ($i - 1) * 1deg + 180deg;
$x: cos($angle) * $d;
$y: sin($angle) * $d;
transform: translate($x, $y) rotate(0deg) ;
}
}
}
}
Case Study
经常用到的场景大概就这些吧,再以一个案例分析来复习一下。
前两天在 Codepen 首页看到热门推荐,作者用存 CSS 动画来实现一个行走的动画,挺新颖的,然而仔细一看,脚步的动画真心觉得别扭,于是想用三角函数优化一下。

绘制头部:
drawHead (t) {
ctx.save()
ctx.beginPath()
ctx.translate(0, Math.sin(t) * 4)
ctx.arc(80, -35, 35, 0, 2 * Math.PI)
ctx.fill()
ctx.closePath()
ctx.restore()
}
我会给每个方法传入周期参数 t, t 从 0 到 2PI , 这样能保证所有的周期运动时间同步。

身体和阴影的绘制都差不多,直接跳过看脚步动画。
脚有两只,按道理应该是抬脚到落脚的动作完成时,其他部位都完成了一个完整的周期,所以在绘制脚的时候,t 需要除以 2。然后第一只脚和第二只脚相差半个脚自身的周期,可以直接将 t 替换成 t + Math.PI 就是第二脚的动画。
drawFeet (t) {
t = t / 2
ctx.translate(Math.cos(t) * -50, 0)
// 另一只脚
ctx.translate(Math.cos(t + Math.PI) * -50, 0)
}

脚步动画自身周期的一半是在地面上的,可以通过判断一下 sin 值,小于 0 则不做 y 纵轴方向上的变化。
ctx.translate(Math.cos(t) * -50, Math.sin(t) > 0 ? Math.sin(t) * -35 : 0)

还没完,为了让脚更加逼真,同样在前半个周期做一下 rotate 。
if (t < Math.PI) {
ctx.rotate(Math.sin(t) * Math.PI / 180 * -5)
}

最终得到的效果是这样的:
总结
现如今前端发展速度非常迅速,刚入门的同学刚学完 jQuery 就被告知,You Dont Need jQuery。追新的脚本根本停不下来,在学习新框架新技能的同时,也别忘了基础知识的重要性。
好了,今天就分享到这里,希望一次汇集这么多效果,能让你下次使用三角函数更得心应手。
以上大部分代码都可以在我的 Codepen 主页看到。
